Question

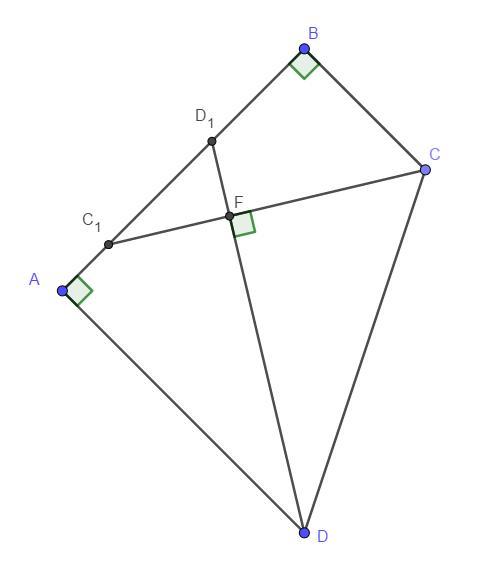
(18 БАЛЛОВ) В четырехугольника АВСD углы А и В равны 90 градусов. Докажите, что биссектрисы двух других углов четырехугольника пересекаются под прямым углом.​

Answer 1

Сумма углов четырехугольника равна 360°, т.е.

$\angle ADC+\angle BCD=180^\circ$

Так как $CC_1,~ DD_1$ - биссектрисы углов $BCD,~CDA$ соответственно, то $\angle BCC_1=\angle C_1CD;~ \angle CDD_1=\angle D_1DA$. Рассмотрим треугольник CDF: сумма углов треугольника равна 180°

$\angle DFC+\angle FCD+\angle CDF=180^\circ\\ \\ \angle DFC+\frac{1}{2}\angle BCD+\frac{1}{2}\angle CDA=180^\circ\\ \\ \angle DFC+\frac{1}{2}(\angle BCD+\angle CDA)=180^\circ\\ \\ \angle DFC+\frac{1}{2}\cdot 180^\circ=180^\circ\\ \\ \angle DFC=90^\circ$

Доказано.