Предмет: Математика,
автор: Dushzhanov987
найти предел:
(в знаменателе корень кубический)
Приложения:
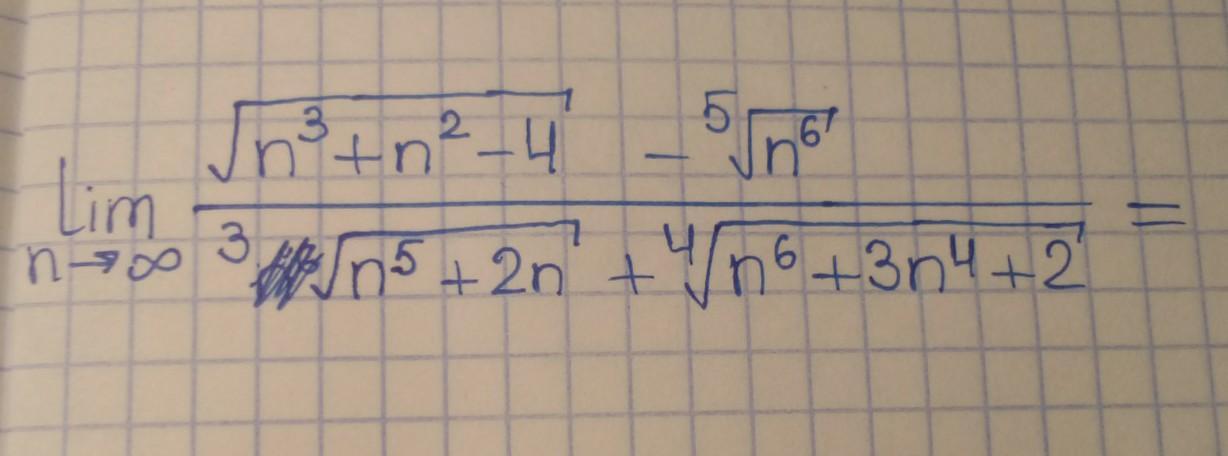
Ответы
Автор ответа:
2
Похожие вопросы
Предмет: Физика,
автор: vyvyvvyvyvyv
Предмет: Русский язык,
автор: ArchiePlay
Предмет: Математика,
автор: krispykris2010
Предмет: Литература,
автор: nonem11
Предмет: Математика,
автор: Chocopie100500