Предмет: Алгебра,
автор: kettte23
Поясніть будь ласка покроково, бо не до кінця розумію що робити з множниками перед модулями
Приложения:
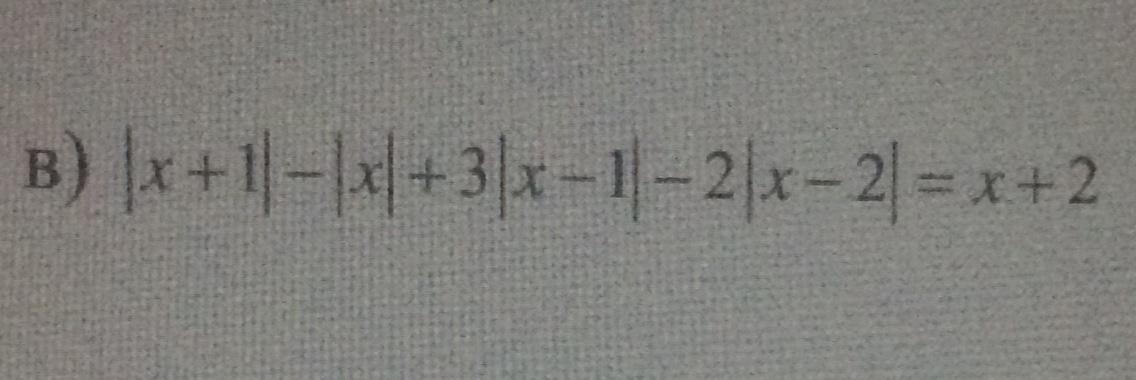
Ответы
Автор ответа:
2
Объяснение:
Получили 5 интервалов. Теперь будем считать знаки каждого модуля на каждом интервале. Если выражение под знаком модуля отрицательно, то модуль раскрываем со знаком минус, если положительно, то со знаком плюс.
Похожие вопросы
Предмет: Математика,
автор: ivanmartynov
Предмет: Математика,
автор: Olga1KH
Предмет: География,
автор: oljaloshuk92
Предмет: Алгебра,
автор: 1401Tamara