у рівнобедренному триутнику основа і висота проведена до основи =4 см .знайти площу круга описаного навколо трикутника. СРОЧНО
Ответы
Ответ: 6,25п см2.
Объяснение:
Площадь круга равна S = пR^2, где R - радиус окр.
Так как треугольник АВС - равнобедренный, AK - высота и медиана. Значит, BK = KC = 4/2 = 2 cм.
Из треуг. АВК (/_К = 90°) находим AB: АВ = AC = корень из (2^2 + 4^2) = корень из (4 + 16) = корень из 20 = 2 корня из 5.
Запишем формулы нахождения площади треугольника:
1) S=1/2 a×h, где а - сторона тр., h - высота, опущенная к стороне а;
2) S = abc/4R, где a, b, c - стороны треугольника, R - радиус описанной окр.
Из первой формулы получаем: S = 0,5 × 4 × 4 = 8
Из второй формулы получаем, что R = abc/4S; имеем: R = (4 × 2к5 × 2к5)/4×8 = 4×4×5/32=2,5.
Тогда площадь круга, описанного вокруг треугольника равна S = (2,5)^2 п = 6,25п см2.
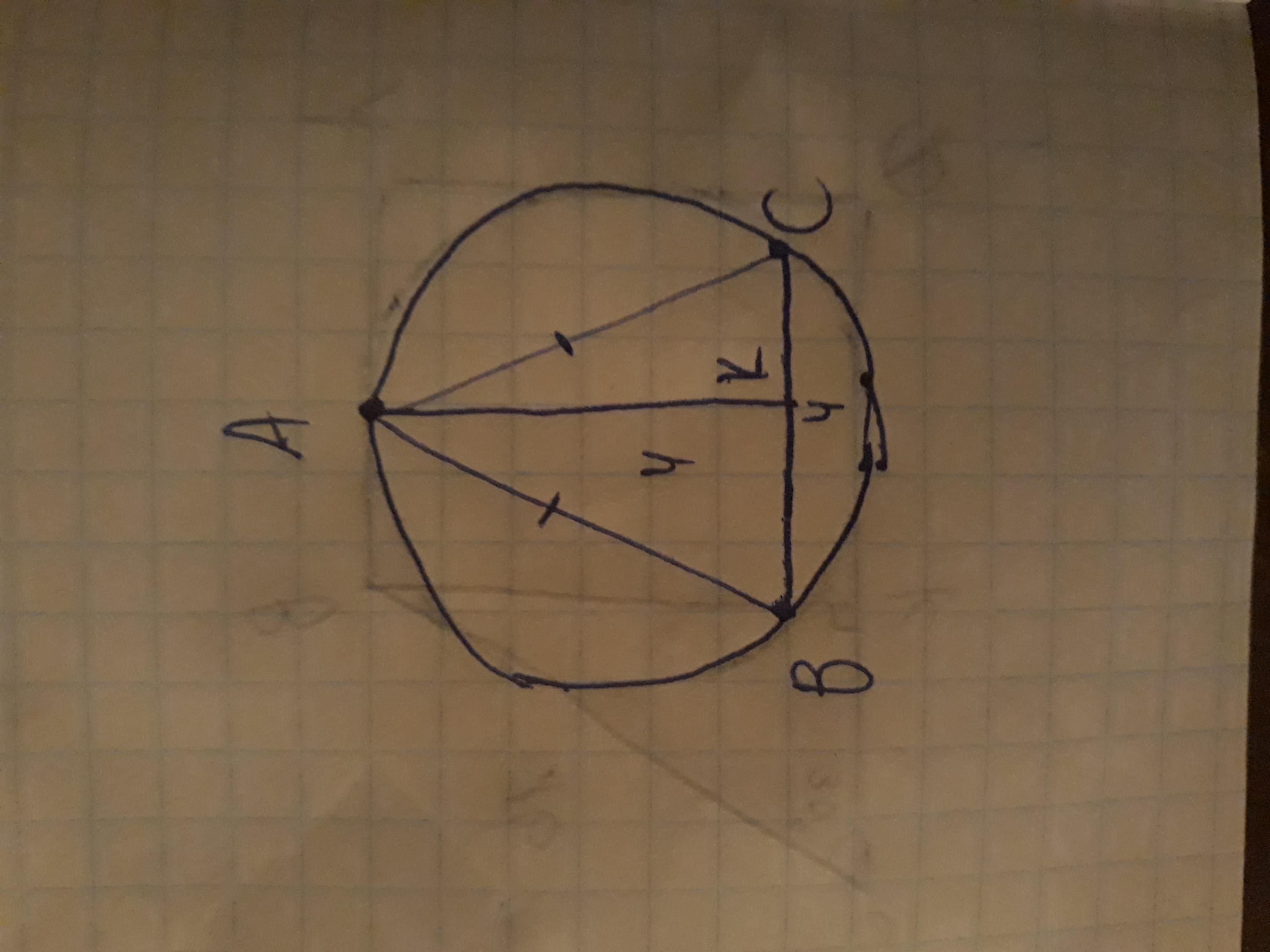
Боковая сторона треугольника, составленного из высоты, половины основания и боковой стороны, по теореме Пифагора равна√(4 ²+2²) =√20=2√5(см)
Учтено, что высота будет и медианой, т.к. проведена к основанию. Значит, ее половина равна 2см.
Площадь треугольника равна 4*4/2=8(см²), с другой стороны, та же площадь через радиус описанной окружности равна а*в*с/(4R), то есть 2√5*4*2√5/(4R)=20/R, значит, 20/R=8, откуда R=20/8=5/2=2.5
Площадь описанного круга равна πR²=π*2.5²=6.25π(см²)