пожалуйста помогите решить
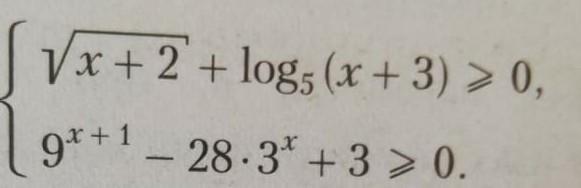
Ответы
как решать первое уравнение совершенно непонятно , кроме того что найдем ОДЗ
подкоренное выражение неотрицательно x + 2 ≥ 0 x ≥ -2
и тело логарифма больше 0 x + 3 ≥ 0 x ≥ - 3
итого x ≥ -2
решим второе и посмотрим потом как решения второго неравенства оказывают влияние на первое
9^(x + 1) - 28 * 3^x + 3 ≥ 0
9*9^x - 28 * 3^x + 3 ≥ 0
3^x = t > 0
9t² - 28t + 3 ≥ 0
D = 28² - 4*3*9 = 784 - 108 = 676 = 26²
t12 = (28 +- 26) / 18 = 3 1/9
(9t - 1)(t - 3) ≥ 0
++++++++[1/9] --------------------- [3] ++++++++++
t≤ 1/9
t≥1
1. 3^x ≤ 1/9
x ≤ -2
2. 3^x ≥ 3
x ≥ 1
x ∈ (-∞ -2] U [1 +∞)
смотрим на ОДЗ
в первой части x ≤ - 2 и ОДЗ x ≥ -2 одна точка совпадает точка -2
смотрим вторую часть x ≥ 1
минимальное значение будет при x = 1 потом будет только возрастать так как √(х+2) и log(5) (x+3) возрастающие функции и скмма возрастающих - сама возрастаюшая
итак минимум √(1 + 2) +log(5) (4) = √3 + log(5) 4 > 0 так как корень больше 0 и логарифм больше 0
итак вся вторая часть удовлетворяет
Ответ x ∈ {-2} U [1 +∞)
Поможешь мне, пожалуйста?