Предмет: Алгебра,
автор: hfhfghfg95
Помогите решить пожалуйста
Приложения:

Ответы
Автор ответа:
1
Область определения функции - те значения х, на которых функция имеет смысл. В данном случае у нас корень четной степени (2-ой), то есть подкоренное выражение должно быть неотрицательным.
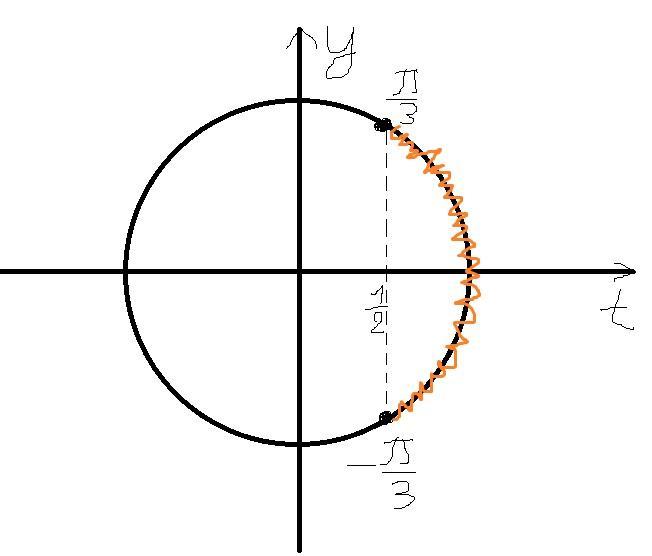
На окружности я отметил ту часть дуги, для которой выполняется (для t) неравенство
Получаем
Делаем обратную замену и получаем решение для х
Что вообще это значит? Это бесконечное объединение отрезков.
Удобнее их записывать, как это было сделано чуть выше.
Ответ:
Приложения:
Похожие вопросы
Предмет: Физика,
автор: Аноним
Предмет: Геометрия,
автор: benebeblin
Предмет: Английский язык,
автор: 11alexan77
Предмет: Математика,
автор: школьник15111630