Question

Помогите, подробное решение!!

Answer 1

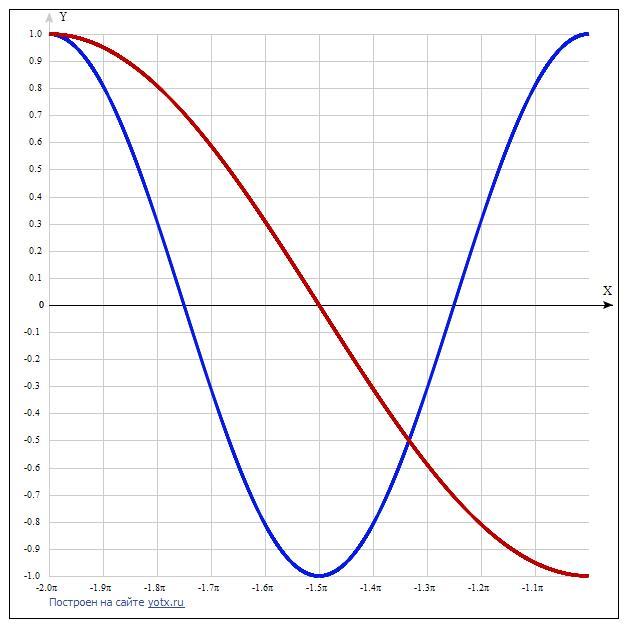
Дано уравнение cos(2x) = sin(x + (π/2)).

С учётом формул приведения оно равноценно уравнению:

cos(2x) = cos(x).

Заменим косинус двойного угла: 2cos²(x) - 1 = cos(x).

Введём замену: cos(x) = t и получим квадратное уравнение:

2t² - t - 1 = 0.    D = 1 - 4*2*(-1) = 9.   x1 = (1 - 3)/(2*2) = -2/4 = -1/2.

x2 = (1 + 3)/(2*2) = 4/4 = 1.

Обратная замена: cos(x) = 1,  х1 = 2πk,  k ∈ Z.

cos(x) -1/2,    x2 = -(2π/3) + 2πk,  k ∈ Z,

                     x3 = (2π/3) + 2πk,  k ∈ Z.

Заданному промежутку соответствуют 2 корня:

k =                                     -1

x_1 = -2π              = -6,2832

x_3 = (2/3)π - 2π  = -4,1888.