Предмет: Алгебра,
автор: 777АЛИНЧИК777
Найдите корни уравнения:
1-х/х+2=х/х-3
Universalka:
Уравнение верно записано ?
Ну да. Если там в задании нет ошибок, то корней нет
Ответы
Автор ответа:
1
Ответ:
Вроде нет корней, если я правильно понял написанное.
Приложения:
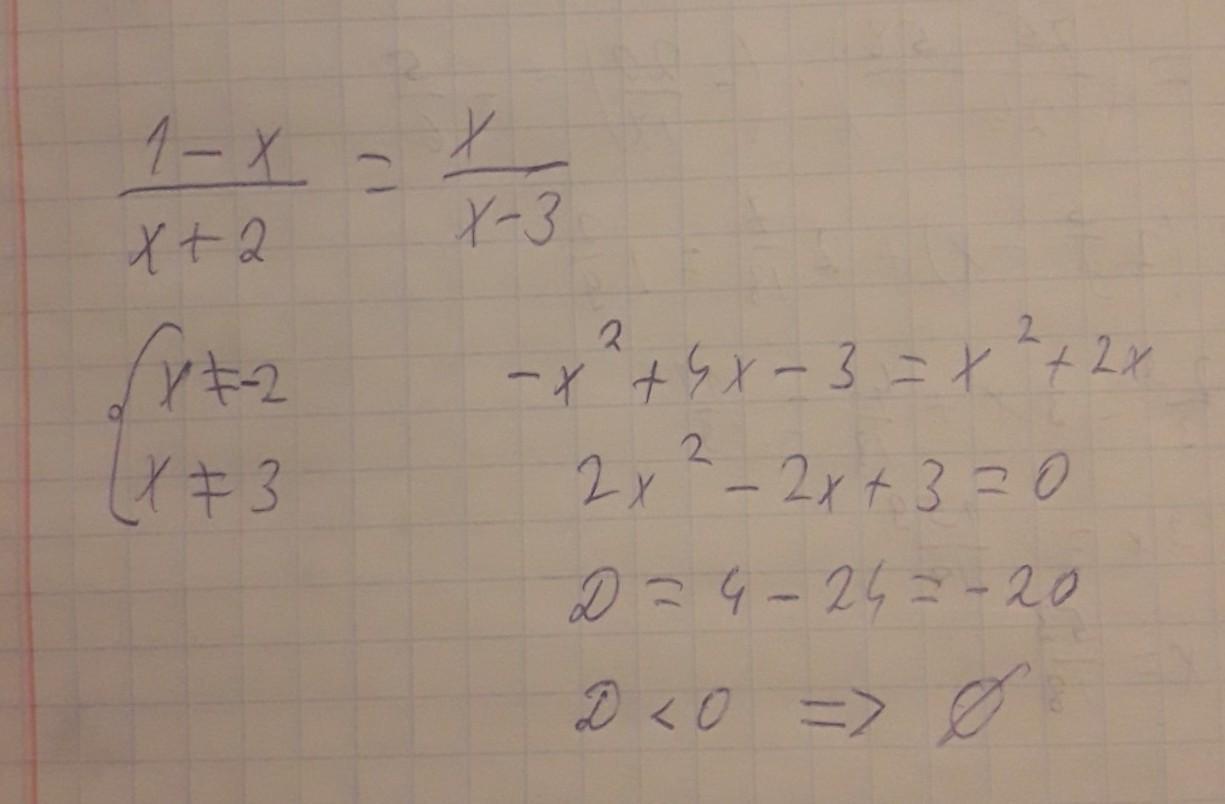
Автор ответа:
7
Дискриминант меньше нулю, значит корней нет.
Похожие вопросы
Предмет: Литература,
автор: lahinasona56
Предмет: Биология,
автор: anastasiyarybina55
Предмет: Химия,
автор: polinarosso
Предмет: Математика,
автор: ЛюбимаяВафля11