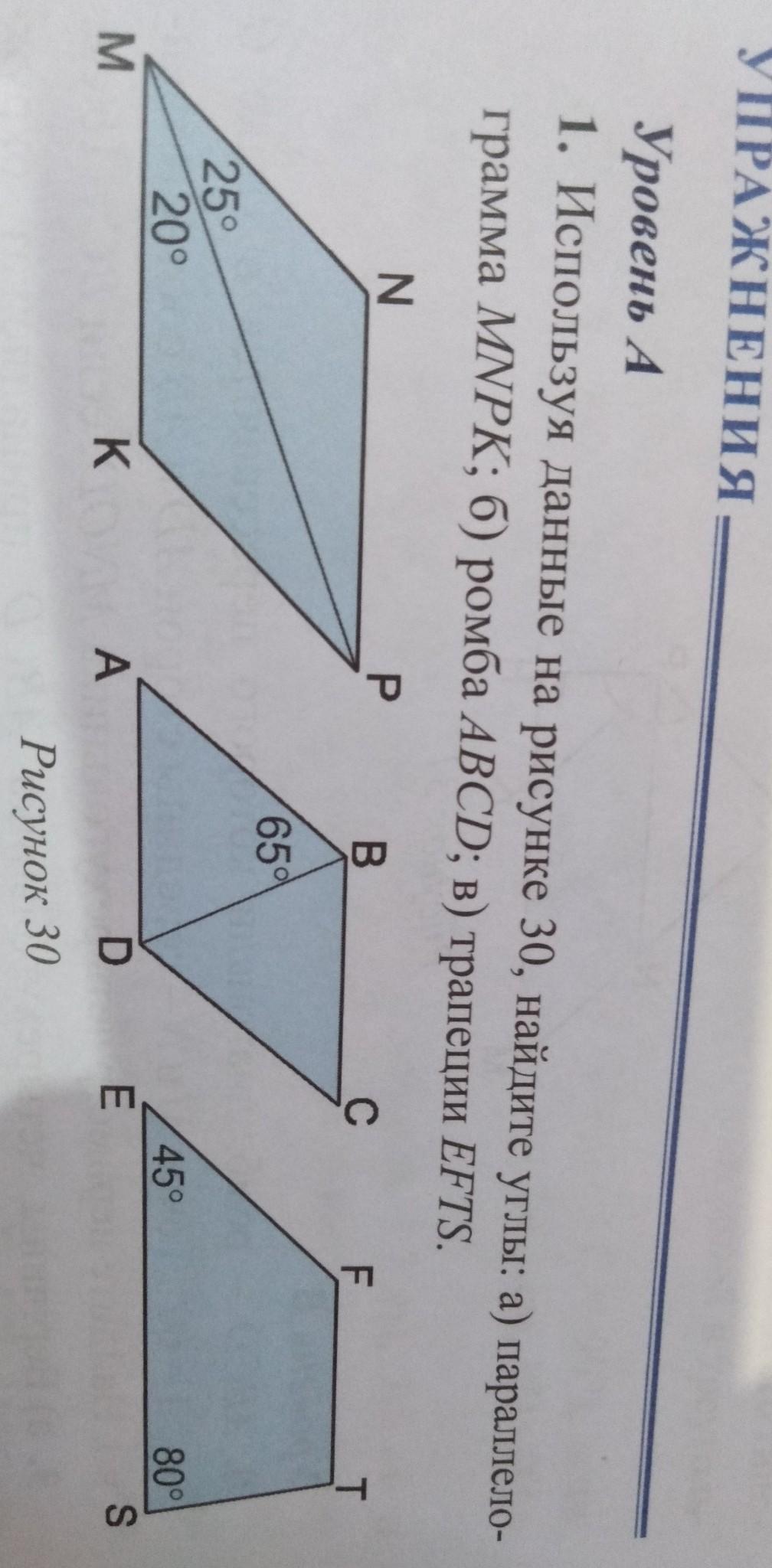
1. Используя данные на рисунке 30, найдите углы: а) параллелограмма MNPK; б) ромба ABCD; в) трапеции EFTS.
СРОЧНО ПОЖАЛУЙСТА!!!
Ответы
а)
Дано :
Четырёхугольник MNPK - параллелограмм.
MP - диагональ.
∡NMP = 25°.
∡PMK = 20°.
Найти :
∡M = ?
∡N = ?
∡P = ?
∡K = ?
Решение :
∡M = ∡NMP + ∡PMK = 25° + 20° = 45°.
- Сумма соседних углов параллелограмма равна 180°.
То есть -
∡М + ∡N = 180°
∡N = 180° - ∡М
∡N = 180° - 45°
∡N = 135°.
- Противоположные углы параллелограмма равны.
Следовательно -
∡M = ∡P = 45°
∡N = ∡K = 135°.
Ответ :
45°, 135°, 45°, 135°.
- - -
б)
Дано :
Четырёхугольник ABCD - ромб.
BD - диагональ.
∡ABD = 65°.
Найти :
∡A = ?
∡В = ?
∡С = ?
∡D = ?
Решение :
Рассмотрим ΔABD. Так как ABCD - ромб, то AD = AB = BC = DC (по определению ромба), тогда ΔABD - равнобедренный.
- Углы у основания равнобедренного треугольника равны.
Следовательно -
∡ABD = ∡BDA = 65°
Тогда по теореме о сумме углов треугольника -
∡BAD = 180° - (∡ABD + ∡BDA) = 180° - (65° + 65°) = 50°.
- Сумма соседних углов параллелограмма равна 180°.
Следовательно -
∡BAD + ∡АВС = 180°
∡АВС = 180° - ∡BAD
∡ABС = 180° - 50° = 130°.
- Противоположные углы параллелограмма равны.
То есть -
∡А = ∡С = 50°
∡В = ∡D = 130°.
Ответ :
50°, 130°, 50°, 130°.
- - -
в)
Дано :
Четырёхугольник EFTS - трапеция (FT║ES, EF и TS - боковые стороны).
∡FES = 45°.
∡TSE = 80°.
Найти :
∡F = ?
∡Т = ?
Решение :
- В трапеции сумма углов, прилежащих к боковой стороне, равна 180°.
Следовательно -
∡FES + ∡F = 180°
∡F = 180° - ∡FES = 180° - 45° = 135°.
- - -
∡TSE + ∡T = 180°
∡T = 180° - ∡TSE = 180° - 80° = 100°.
Ответ :
135°, 100°.