Question

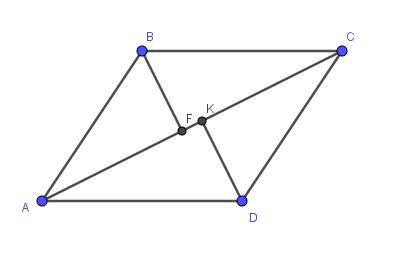
2. В четырехугольнике ABCD к диагонали АС проведены перпен-
дикуляры BF и DK, причем BF = DK, угол BAF = угол DCK. Докажите,
что ABCD – параллелограмм.
​

Answer 1

Прямоугольные треугольники $ABF$ и $CKD$ равны по катету и прилежащему острому углу ($\angle ABF=\angle KDC$). Из равенства треугольников следует, что $AB=CD$

Так как $\angle BAF=\angle DCK$ - накрест лежащие углы равны, то по первому признаку параллельности прямых $AB~\big|\big|~CD$

• Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Следовательно, $ABCD$ - параллелограмм.