Предмет: Алгебра,
автор: Аноним
Решить всё что есть на фото!(Докажите тождество)
Приложения:
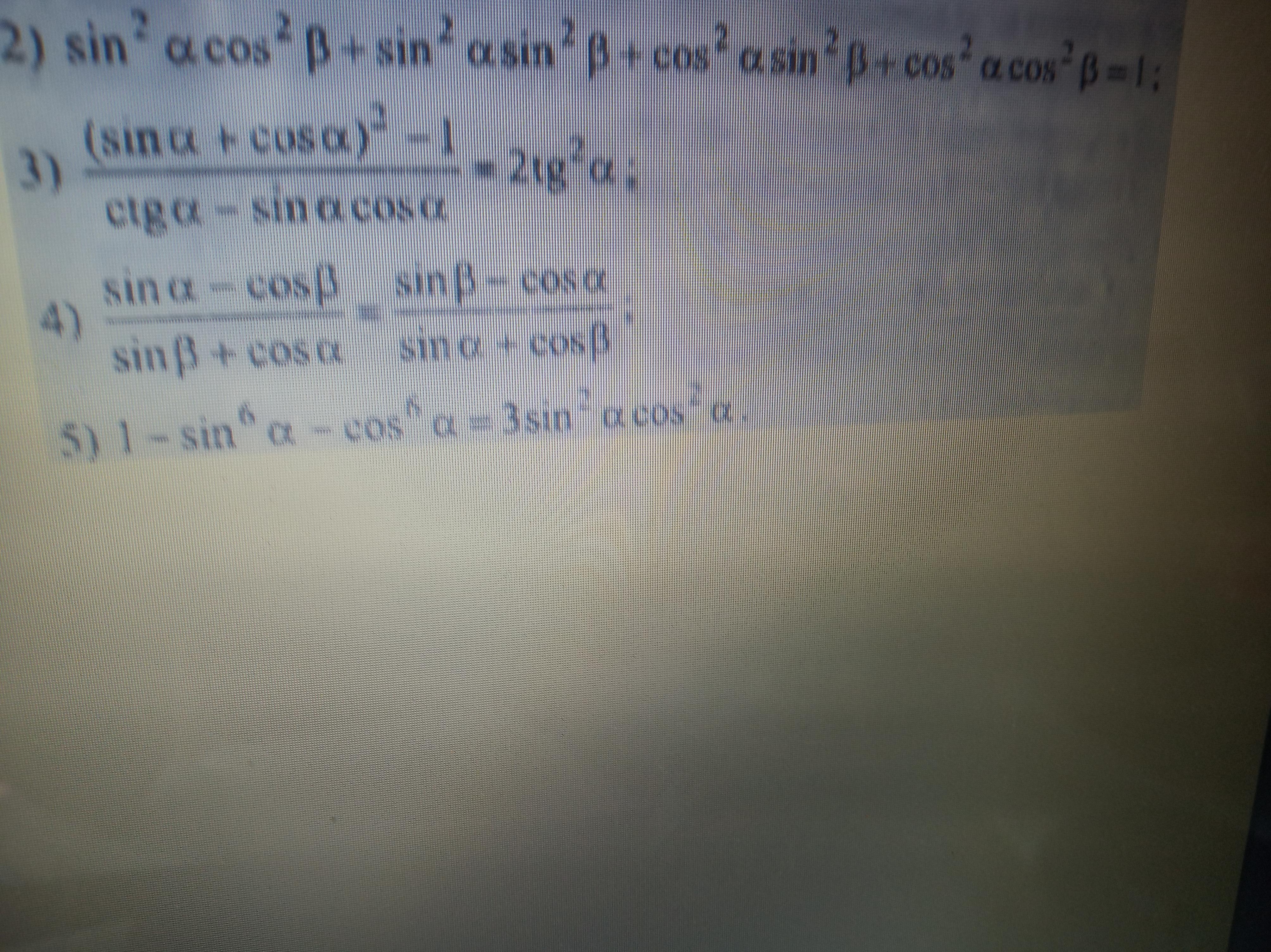
Ответы
Автор ответа:
1
2) (Sin²αCos²β + Sin²αSin²β) + (Cos²αSin²β + Cos²αCos²β) =
= Sin²α(Cos²β + Sin²β) + Cos²α(Sin²β + Cos²β) = Sin²α * 1 + Cos²α * 1 =
= Sin²α + Cos²α = 1
1 = 1
Что и требовалось доказать
Что и требовалось доказать
Разность левой и правой части равна нулю, значит тождество доказано .
Что и требовалось доказать
Похожие вопросы
Предмет: Литература,
автор: kodikpodik21
Предмет: Русский язык,
автор: lisasem
Предмет: Английский язык,
автор: ig39418521
Предмет: Алгебра,
автор: kolkhieva
Предмет: Физика,
автор: Мурад945