Предмет: Геометрия,
автор: nikitapostol2006
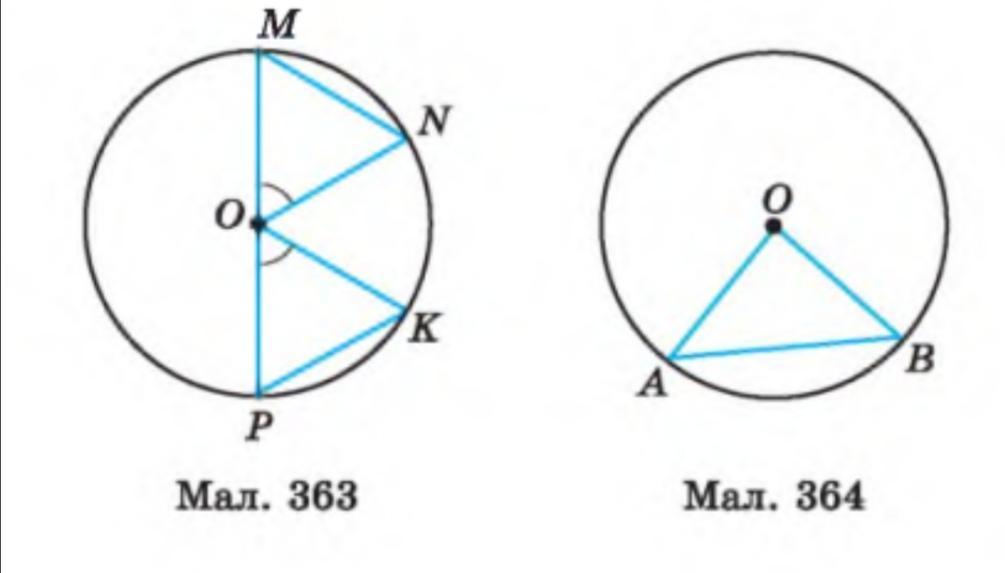
У колі із центром проведено хорди MN і РК та діаметр РМ.
Кути РОК = куту MON (мал. 363). Доведіть, що трикутники MON та РОК рiвнi.
Приложения:
Ответы
Автор ответа:
15
Так как - центр окружности и середина
, то
.
как вписанные углы, опирающиеся на равные отрезки.
Пользуясь тем что сумма углов треугольника равна 180°, можно сделать вывод, что
Треугольники и
равны по стороне и двум прилежащим к ней углам
Похожие вопросы
Предмет: Химия,
автор: arseniibystrov83
Предмет: Английский язык,
автор: nekrasovaana915
Предмет: Математика,
автор: steputka2535
Предмет: Математика,
автор: gulinya
Предмет: Литература,
автор: машенька248