Предмет: Алгебра,
автор: minovaksyushashai
НАЙТИ ПРОИЗВОДНУЮ ФУНКЦИИ
Приложения:
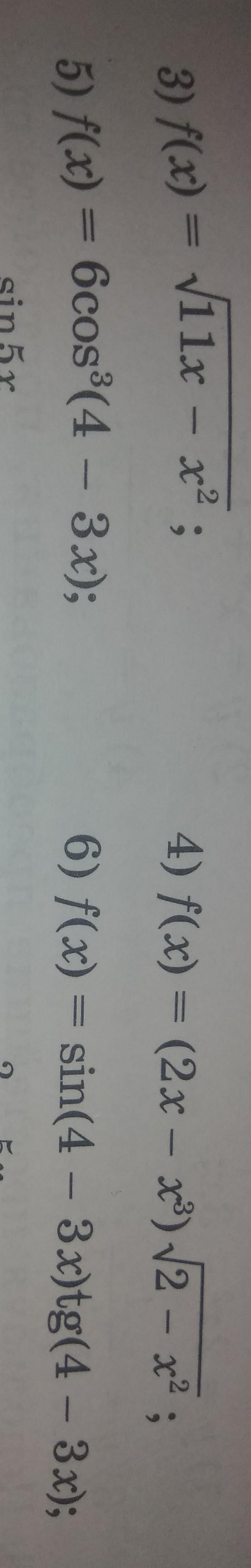
Ответы
Автор ответа:
3
Объяснение:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: originalismail1
Предмет: Литература,
автор: sofinka2010
Предмет: Химия,
автор: user272727
Предмет: Математика,
автор: sofiaIee2007031