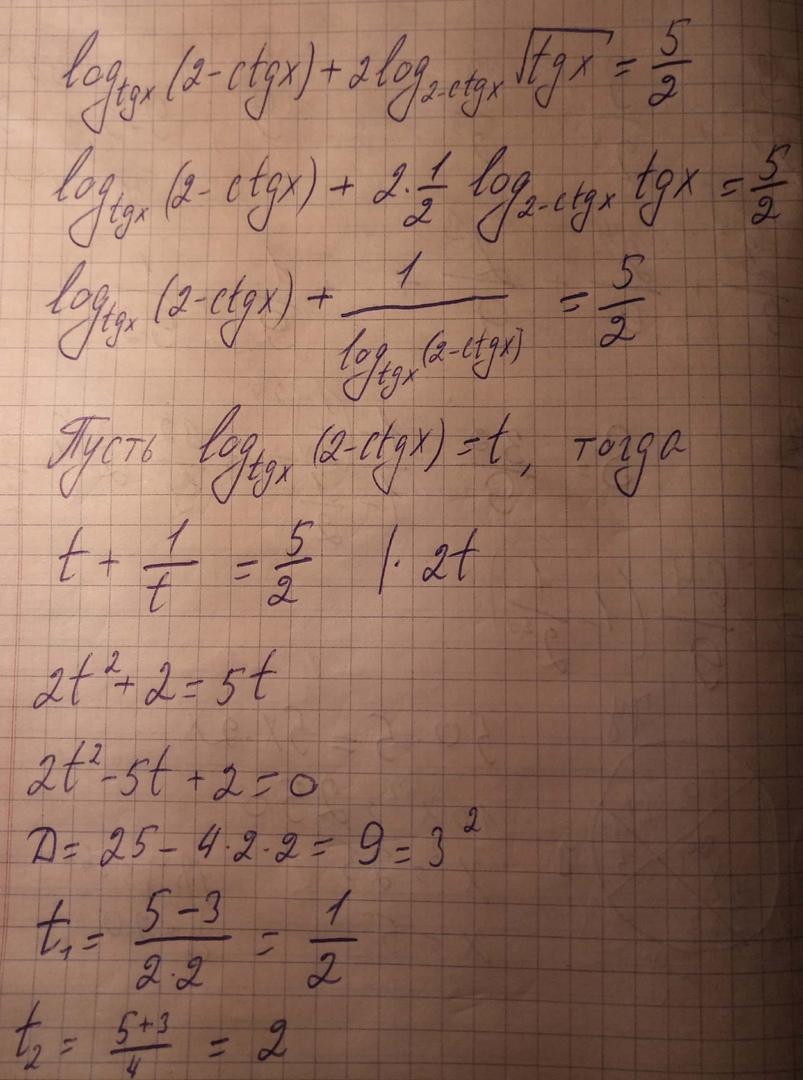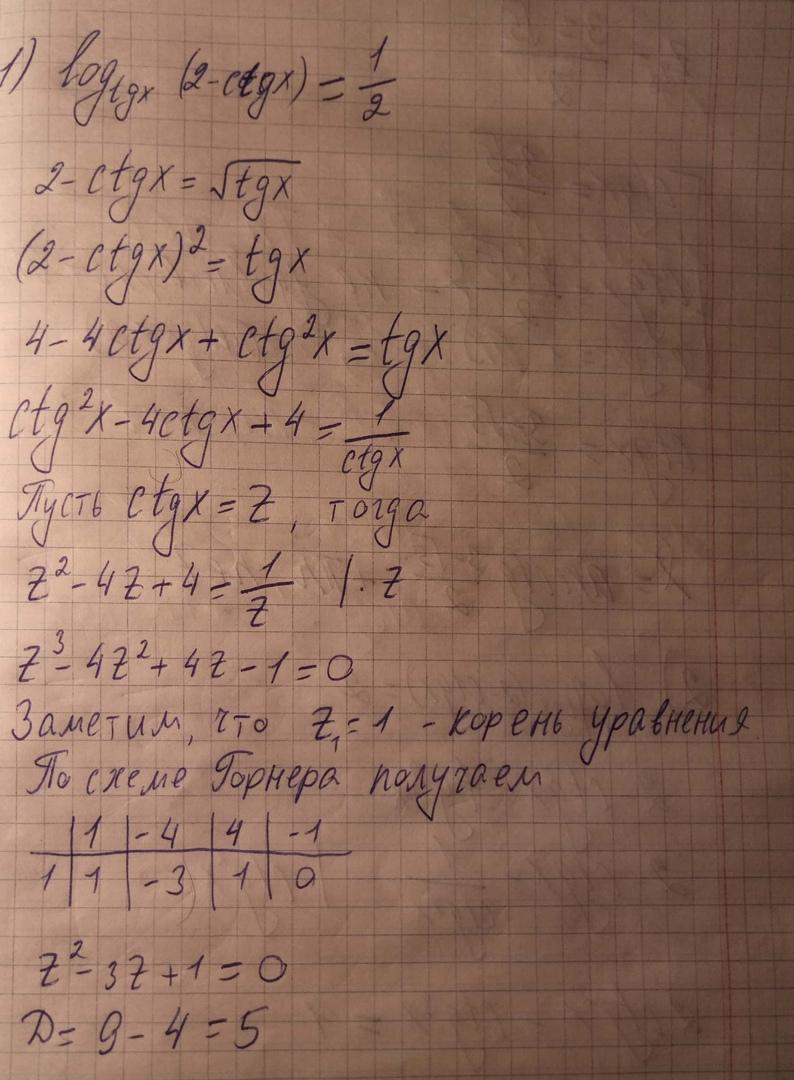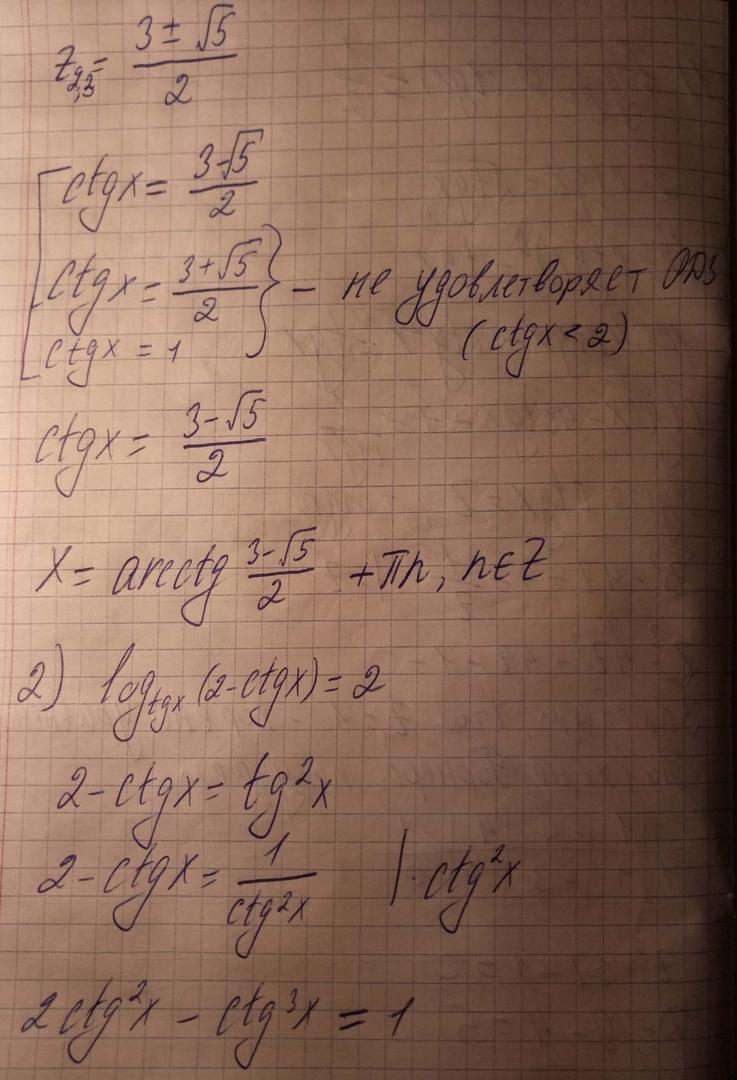Решите уравнение

Ответы
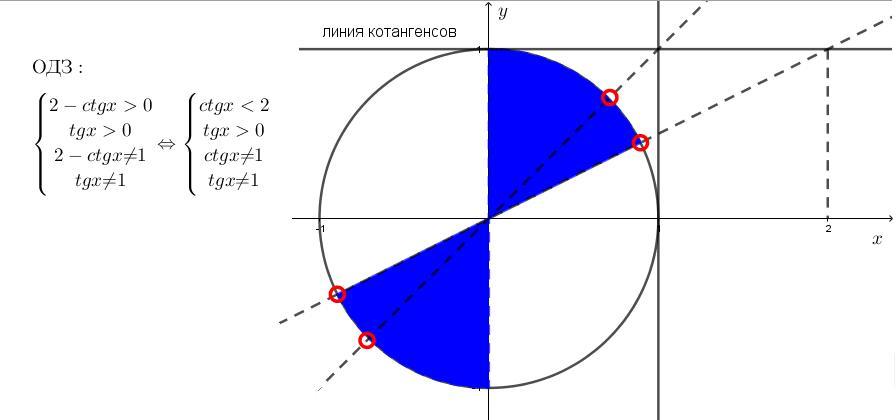
Область определения запишем
Систематизируем немного
Из последнего видим, что , а это уже есть. Остается тогда
Правда, решая неравенство
методом интервалов, получаем
Но тангенс из другого неравенства больше нуля, поэтому
и не забываем
, вот все ограничения.
Теперь решаем неравенство:
Тут t явно не равно нулю в числителе, поэтому это ограничение нам особо не нужно.
Решаем 1-ое уравнение (t=1/2):
Видно по сумме коэффициентов, равно 0, что p=1 - корень уравнения. Однако, , но по ограничениям не подходит. Теперь делим уголком или по схеме Горнера на p-1 и получаем
Видно, что оба значения положительны, но второе и больше 1/2, так как в числителе число, куда больше, чем 1.
А вот другой корень проверим:
, а значит, tgx <1/2 в этом случае и это нам не подходит, отсюда берем лишь
Решаем второе уравнение:
(то, что здесь понятно, поэтому смело на него умножаем все уравнение без потери корней)
Тут сумма коэффициентов равна 0, k=1 - корень. Поделим на k-1 уголком или по схеме Горнера и получим
Корень k=1=tgx нам не подходит, так как по ограничениям
Решаем квадратное уравнение, которое дает нам вторая скобка.
Отрицательный корень не берем, так как
Проверим положительный корень на выполнение ограничений (сравня с 1/2)
Левое выражение больше правого, значит, этот корень удовлетворяет (так как
это не целое число, то оно не равно 1, то есть
, поэтому корень подходит)
Ответ:
ОДЗ на рисунке (решения долны входить в синие секторы)
решение на фото.