Предмет: Алгебра,
автор: toffrry41
Найти производные, кто сможет?
Приложения:
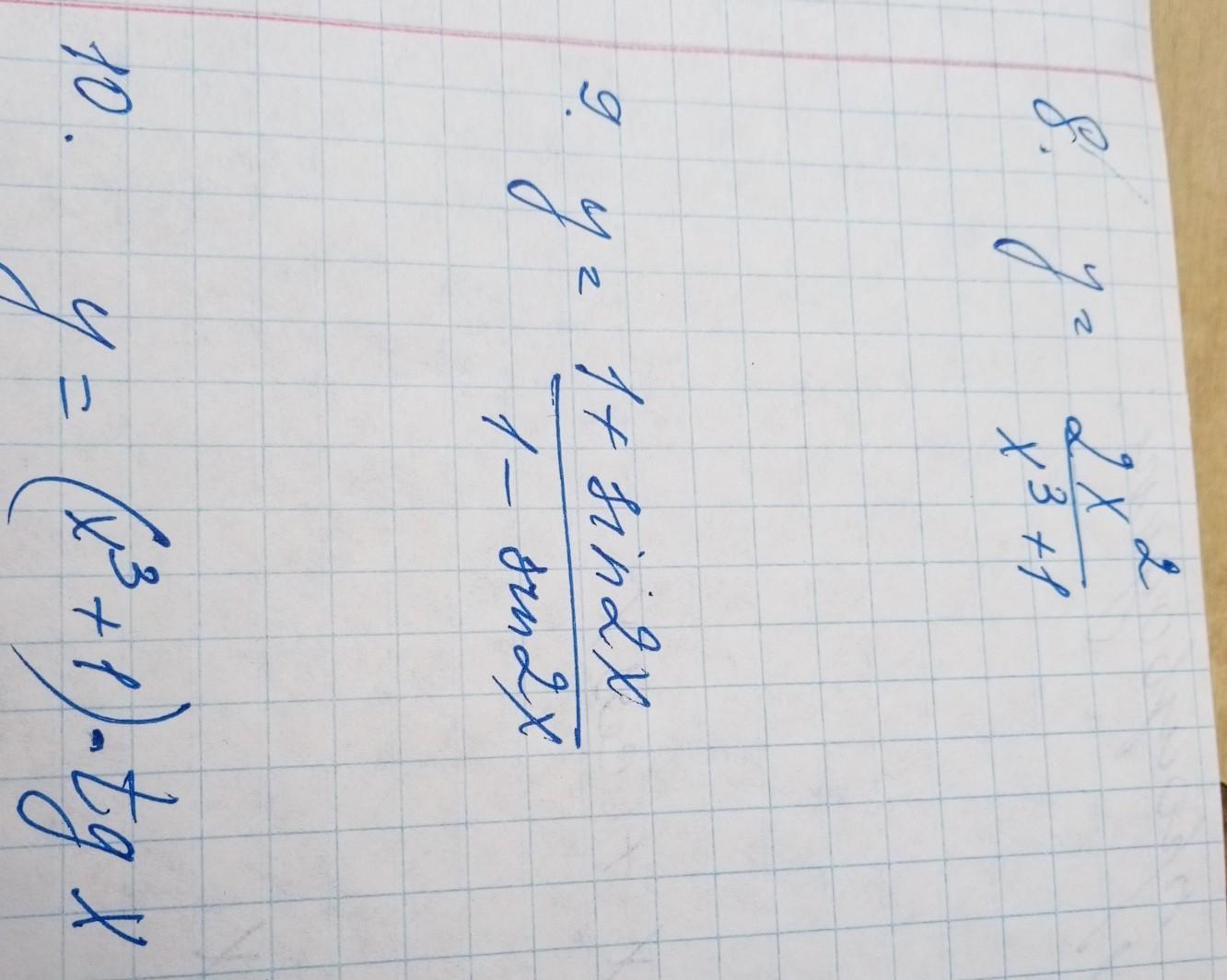
Ответы
Автор ответа:
1
Объяснение:
Похожие вопросы
Предмет: География,
автор: Аноним
Предмет: История,
автор: kontrabanda2229
Предмет: Информатика,
автор: nikitoska200744
Предмет: Геометрия,
автор: Luki0
Предмет: География,
автор: ксюша1196