Предмет: Алгебра,
автор: gacans234
Допоможіть рішити 1.102 і 1.103 даю 30 балів
Приложения:

Ответы
Автор ответа:
0
1.102
1)
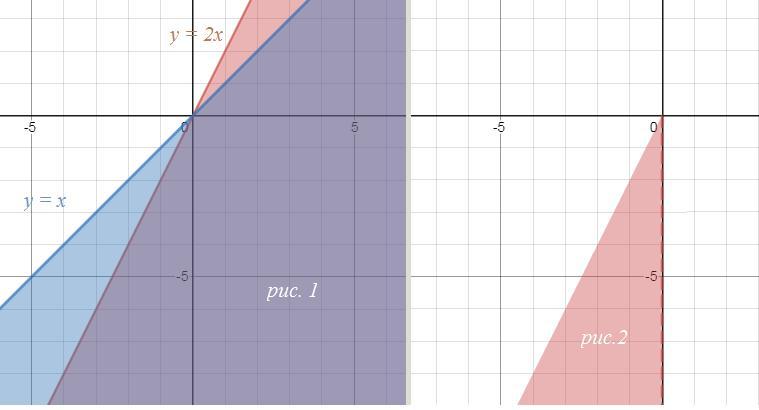
ОДЗ:
{2x - y ≥ 0 ⇒ y ≤ 2x
{x - y ≥ 0 ⇒ y ≤ x
Cм. рис. 1
В условиях ОДЗ возводим обе части неравенства в квадрат:
2х - у < x - y
x < 0
С учетом ОДЗ
О т в е т. на рис. 2
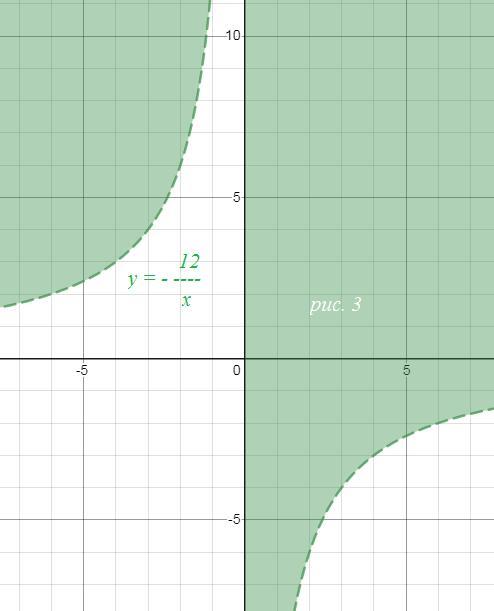
б)
См. рис. 3
1.103
Проверяем для n=1
1·2·3=(1·2·3·4)/4 - верно
Предполагаем, что
равенство верно для n=k
Докажем пользуясь этим равенством, что данное равенство верно и для n=k+1
Выписываем левую часть
Заменяем первые k слагаемых на
получаем сумму:
что и требовалось получить.
На основании принципа матем. индукции равенство верно для любого натурального n
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: nastymi33
Предмет: Литература,
автор: dasadarina98
Предмет: Українська мова,
автор: kakoitonekit
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: DanilGG11