Question

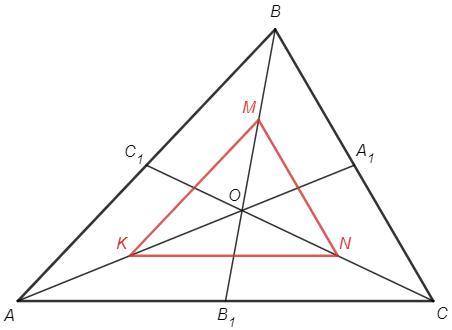
В треугольнике АВС медианы АА¹, ВВ¹, СС¹ пересекаются в точке О. Точки K, M, N являются серединами отрезков АО, ВО, СО соответственно. а) Докажите, что треугольники KMN и АВС подобны.
б) Найдите периметр треугольника АВС, если периметр треугольника KMN – 44 см. Найдите отношение медиан треугольника АВС к медианам треугольника KMN.
Помогите пожалуйста, буду очень благодарна ​

Answer 1

Средняя линия треугольника соединяет середины двух сторон, параллельна третьей стороне и равна ее половине.

Отрезки KM, MN, KN являются средними линиями в треугольниках AOB, BOC, AOC.

a) KM||AB, MN||BC, KN||AC

KMN~ABC по трем параллельным сторонам

б) KM=AB/2, MN=BC/2, KN=AC/2

P(ABC) =2P(KMN) =44*2 =88 (см)

в) Отношение соответствующих отрезков (медиан, биссектрис, высот и любых отрезков, построенных сходным образом) в подобных треугольниках равно коэффициенту подобия.

k=AB/KM =2

Медианы ABC вдвое больше медиан KMN.