Предмет: Математика,
автор: hitman0114
Помогите пожалуйста решить, не могу понять
Приложения:
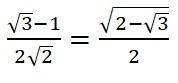
Ответы
Автор ответа:
1
Если докажем равенство числителей, то обе дроби будут равны
Так как
Имеем - верное тождество.
А значит, и исходные дроби равны. Что и требовалось доказать
hitman0114:
Спасибо
Всегда пожалуйста)
Похожие вопросы
Предмет: Английский язык,
автор: sebetkokristina
Предмет: Математика,
автор: fhctybqh
Предмет: Қазақ тiлi,
автор: inozemcevaluciana
Предмет: Алгебра,
автор: Максим2000002