Предмет: Геометрия,
автор: cronnel
помогите с задачей по геометрии пожалуйста
Приложения:
Ответы
Автор ответа:
1
Ответ: 7 см.
Объяснение:
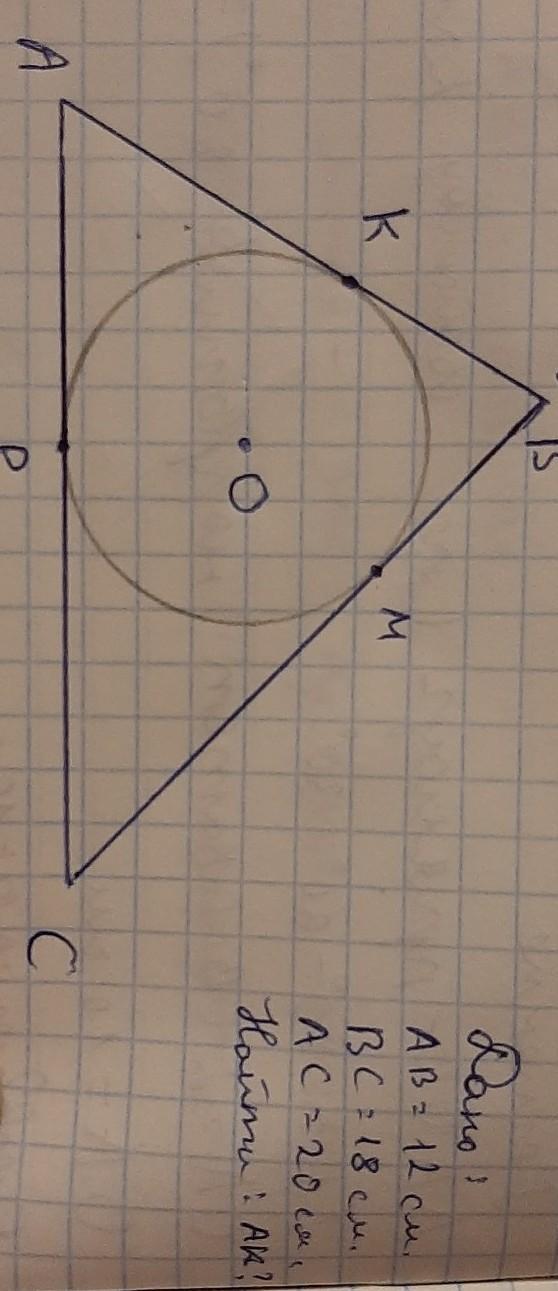
Рассмотрим 2 касательные из одной точки: AB и BC, отрезки касательных равны (по свойству касательных), то есть KB = BM.
Аналогично AK = AP, PC = CM
Пусть AK = x, KB = y, MC = z, составим систему уравнений:
Вычтем из третьего уравнения второе
cronnel:
спасибо
Автор ответа:
0
Отрезки касательных, проведенных из точки вне окружности, к одной окружности, равны.
ВК=ВМ, АК=АР, СМ=СР.
Поэтому АВ+ВС+АС =2*ВК+2*АК+2*СР=12+18+20=50⇒ВК+АК+СР=25.
АВ=АК+КВ, 12=АК+КВ. Значит, СР=25-12=13.
АС=АР+СР⇒20=АР+13⇒АР=20-13; АР=7
ОТВЕТ 7 см.
Похожие вопросы
Предмет: Информатика,
автор: gurlovoleg
Предмет: Математика,
автор: soauwo
Предмет: Геометрия,
автор: M0nika15
Предмет: География,
автор: МгКочегар
Предмет: Обществознание,
автор: toma9779