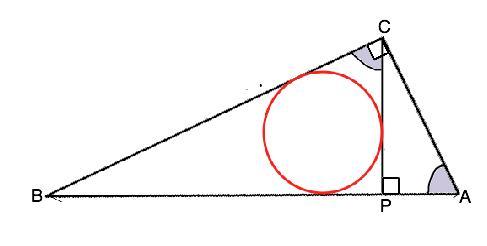
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 24, тангенс угла BAC равен 12/5 Найдите радиус окружности, вписанной в треугольник ABC.
Ответы
Решение приложил /////////////////
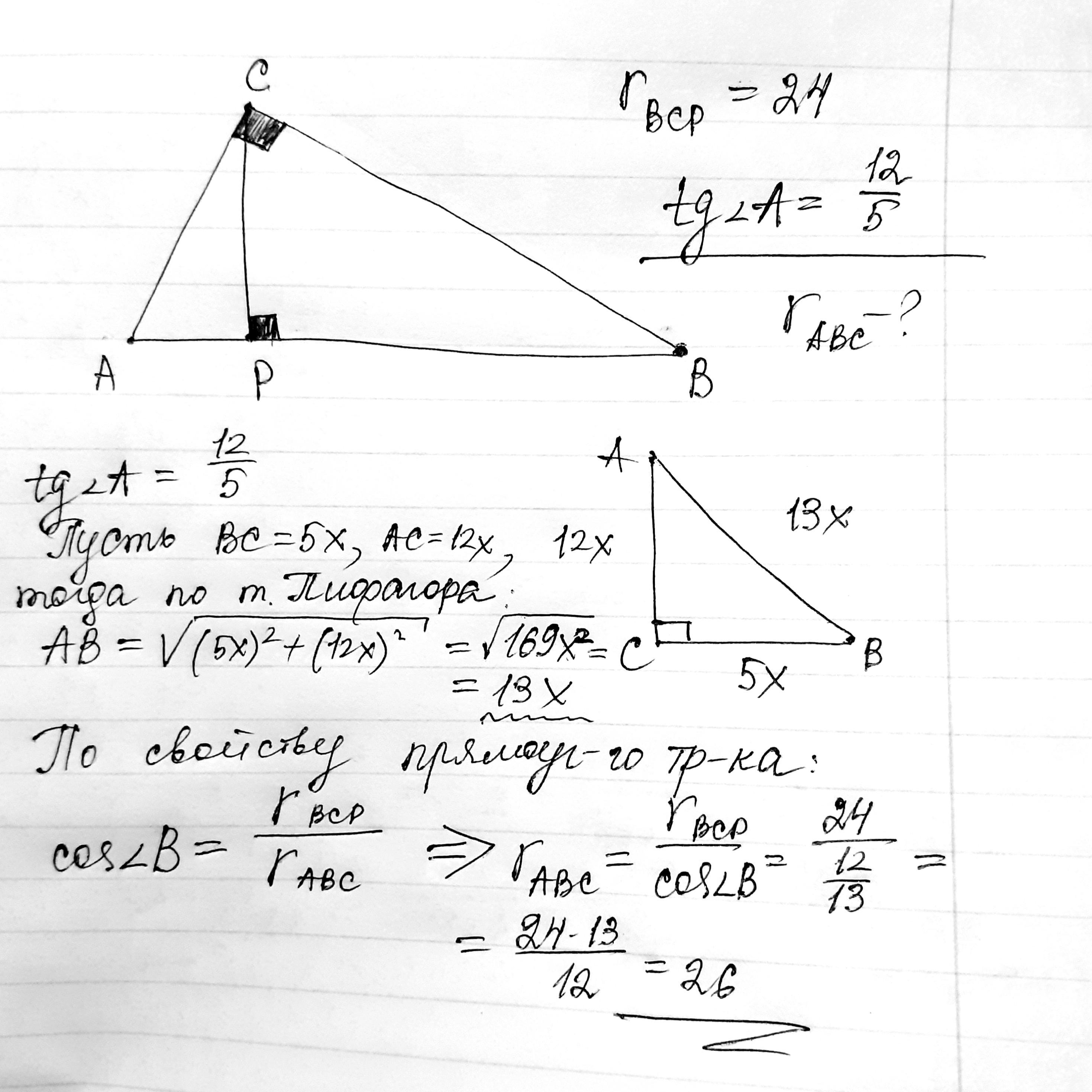
Вариант решения.
Ответ: 26 (ед. длины)
Объяснение:
Вспомним: высота прямоугольного треугольника, проведенная к гипотенузе, делит его на треугольники, подобные друг другу и исходному треугольнику. ⇒ ∆ ВСР ~ ∆ АВС.Отношение сходственных элементов подобных треугольников равно коэффициенту подобия. ⇒
Отношение радиусов окружностей, вписанных в подобные треугольники, равно коэффициенту подобия.
Примем коэффициент отношения сторон треугольника АВС равным а. Тогда ВС=12а, СА=5а. По т.Пифагора или без вычислений найдем АВ=13а ( отношение катетов ∆ АВС из Пифагоровых троек 5:12:13)
Из подобия ∆ ВСР и АВС коэффициент подобия их гипотенуз k=ВС:АВ=12/13, откуда r(ВСР):r'(АВС)=12/13
24:r'=12/13
r'(ABC)=24•13/12=2•13=26 (ед. длины)