Question

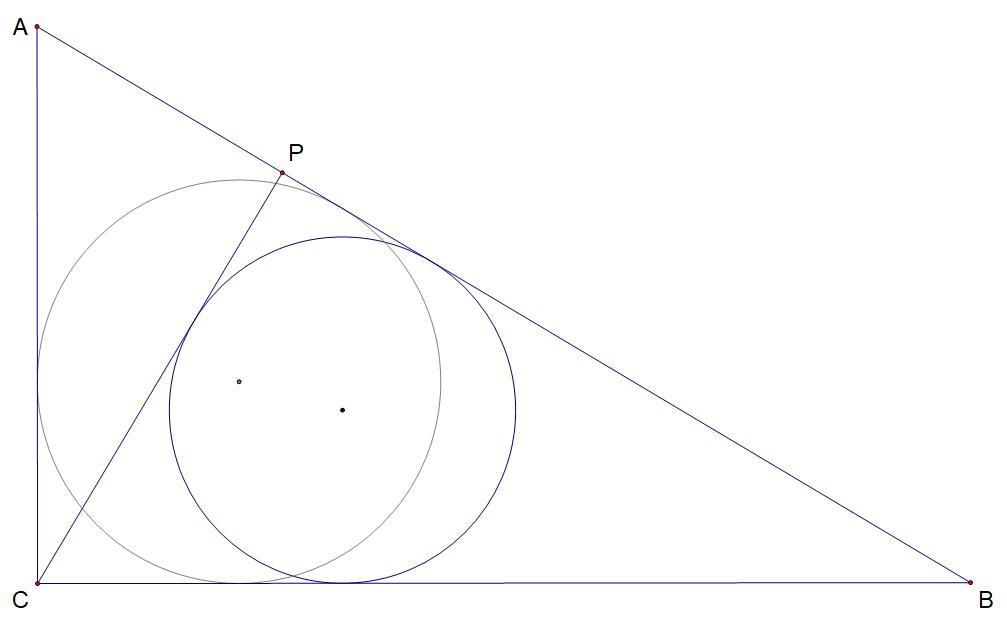
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 24, тангенс угла BAC равен Найдите радиус окружности, вписанной в треугольник ABC.

Answer 1

на фото....................

Answer 2

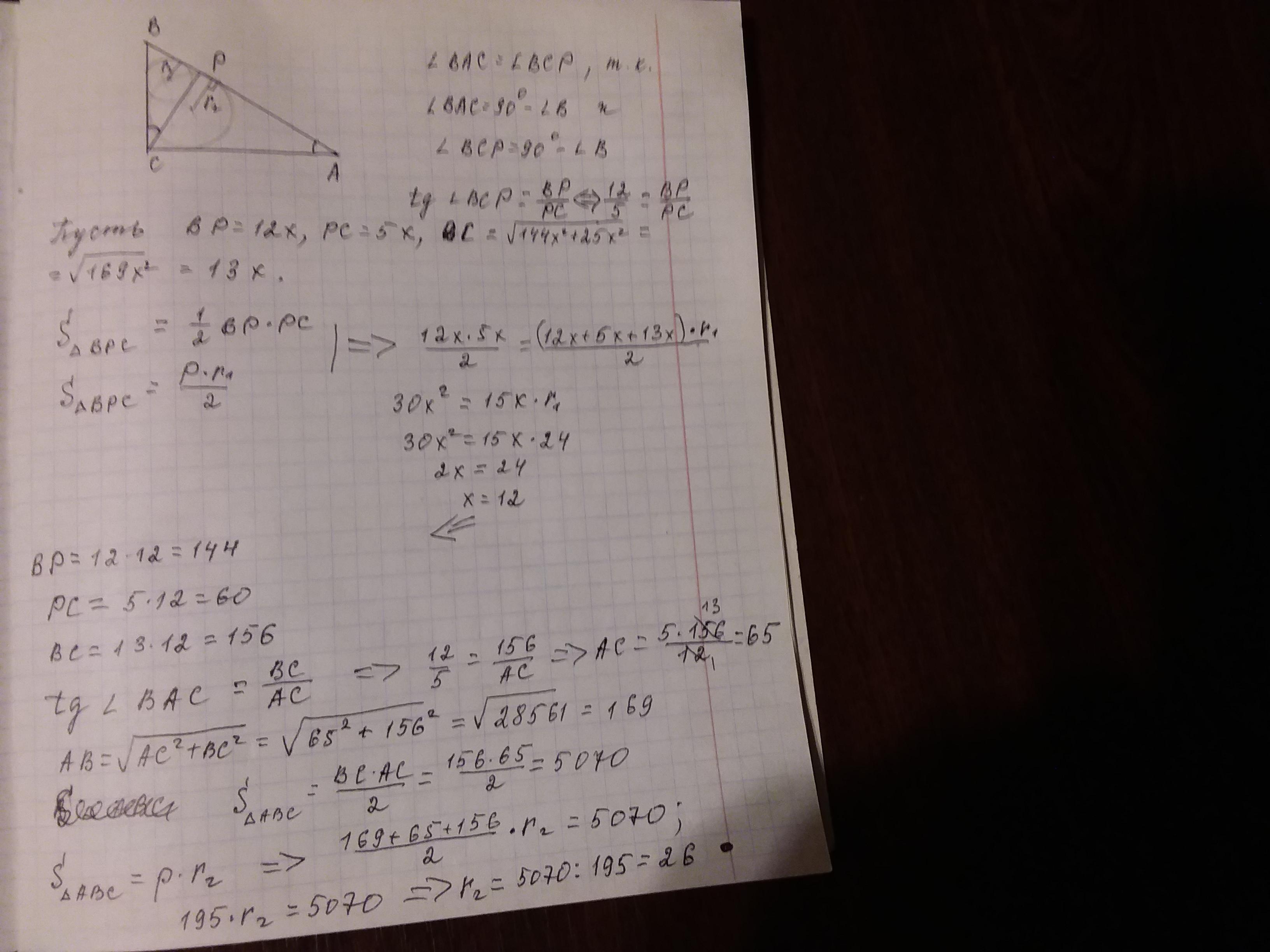
Ответ: 26

Объяснение:

Пусть r -- радиус вписанной окружности в ΔBCP, а R --  радиус вписанной окружности в ΔBAC

1.

tg∠BAC = 12/5, откуда по определению тангенса

$\frac{BC}{AC}=\frac{12}{5}$

Пусть BC = 12x, тогда AC = 5x

По теореме Пифагора найдём AB:

$AB=\sqrt{AC^2+BC^2}=\sqrt{25x^2+144x^2}=\sqrt{169x^2}=13x$

2.

tg∠CAP = 12/5, по определению тангенса из ΔACP

$\frac{CP}{AP}=\frac{12}{5}$

Пусть CP = 12y, тогда AP = 5y

Составим уравнение с помощью теоремы Пифагора в ΔACP и выразим y через x:

$AC^2=CP^2+AP^2\\ \\ (5x)^2=(12y)^2+(5y)^2\\ \\ 25x^2=144y^2+25y^2\\ \\ 169y^2=25x^2\\ \\ y^2=\frac{25x^2}{169} \\ \\ y=б\frac{5x}{13}$

Отрицательным y быть не может, так как он выражает длину отрезка, следовательно y = 5x/13, откуда

$CP=12y=\frac{60x}{13}\\ \\ AP=5y=\frac{25x}{13}$

3. Выразим через x сторону BP, периметр и площадь ΔCPB:

$PB=AB-AP=13x-\frac{25x}{13}=\frac{169x-25x}{13}=\frac{144x}{13}$

$P \Delta CPB=CP+PB+CB=\frac{60x}{13}+\frac{144x}{13}+12x=\frac{60x+144x+156x}{13}=\frac{360x}{13}$

$S \Delta CPB=\frac{1}{2}\cdot CP\cdot PB =\frac{1}{2}\cdot \frac{60x}{13}\cdot \frac{144x}{13}=\frac{30\cdot144x^2}{169}$

4. Используя формулу площади через радиус вписанной окружности составим уравнение:

$S \Delta CPB=\frac{P \Delta CPB}{2} \cdot r\\ \\ \frac{30\cdot144x^2}{169}=\frac{360x}{13\cdot 2}\cdot24\\ \\ \frac{30\cdot144x}{169}=\frac{360\cdot24}{13\cdot 2}\\ \\ x=\frac{360\cdot12}{13}:\frac{30\cdot144}{169}\\ \\ x=\frac{30\cdot12\cdot12}{13}\cdot \frac{169}{30\cdot144}\\ \\ x=13$

5. Используя найденный x, вычислим периметр и площадь ΔABC:

PΔabc = AB + BC + AC = 13x + 12x + 5x = 30x = 30*13

SΔabc = 1/2 * AC * CB = 1/2 * 5x * 12x = 30x² = 30*13²

6. Найдём R, составив уравнение по формуле S = P/2 * R

$30\cdot 13^2=\frac{30\cdot 13}{2} \cdot R\\ \\ R=(30\cdot 13^2):(15\cdot 13)\\ \\ R=13\cdot 2\\ \\ R=26$