Question

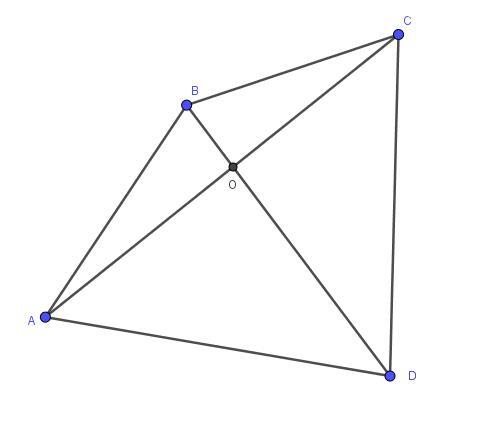
Диагонали четырёхугольника ABCD пересекаются в точке 0. Площади треугольников ABO, BCO,COD равны 3,5,2. Найдите площадь AВСD

Answer 1

на фото...................

Answer 2

У треугольников $DAO$ и $BAO$ высоты, опущенные из вершины А равны, то если высоты двух треугольников равны, то их площади относятся как основания.

$\dfrac{S_{DAO}}{S_{BAO}}=\dfrac{OD}{OB}$

Аналогично, у треугольников $BCO$ и $COD$ высоты, опущенные из вершины С равны, следовательно, $\dfrac{S_{BCO}}{S_{COD}}=\dfrac{OB}{OD}$

Тогда $\dfrac{S_{BAO}}{S_{DAO}}=\dfrac{S_{BCO}}{S_{COD}}~~\Rightarrow~~ S_{DAO}=\dfrac{S_{BAO}\cdot S_{COD}}{S_{BCD}}=\dfrac{3\cdot 2}{5}=1.2$

$S_{ABCD}=S_{DAO}+S_{ABO}+S_{BCO}+S_{COD}=1.2+3+5+2=11.2$ кв. ед.

Ответ: 11.2 кв. ед.