Предмет: Математика,
автор: futi4582
Дам 15 баллов
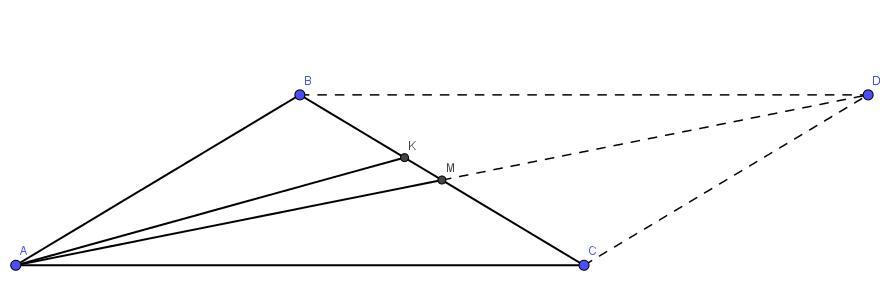
В равнобедренном треугольнике ABC с тупым углом B и основанием AC = 30 проведены биссектриса AK и медиана AM , при этом KM = 2 . Найдите боковую сторону и медиану AM .
Аноним:
20 это боковая сторона
AM = 5 * sqrt(22)
Ответы
Автор ответа:
2
Так как АМ - медиана, то BM = CM отсюда CM = BK + KM.
По свойству биссектрисы:
По теореме Виета
- не удовлетворяет условию;
Тогда длина боковой стороны:
Достроим до параллелограмма ABDC, имеем AD = 2AM
Сумма квадратов длин диагоналей параллелограмма равна сумме квадратов всех его сторон
Ответ: 20 и AM = 5√22
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: julia770627
Предмет: Биология,
автор: kakashka80
Предмет: Математика,
автор: kukuruzav21
Предмет: Математика,
автор: 1945104
Предмет: Информатика,
автор: elektreck