Предмет: Геометрия,
автор: 140539lil
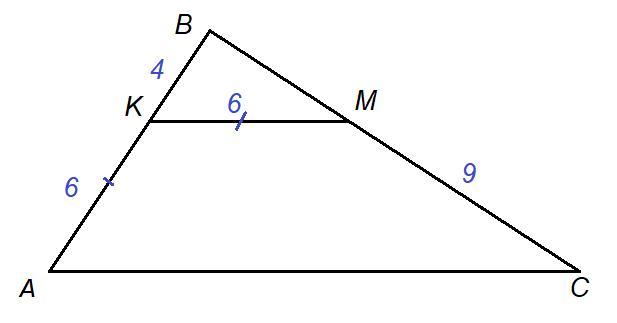
Дан треугольник ABC, точки K и M принадлежат сторонам AB и BC соответсвенно, KM || AC. Найдите периметрт реугольника ABC, если BK = 4см, AK = KM = 6см, MC = 9см.
Если кто может, решите.
Аноним:
40
Ответы
Автор ответа:
3
Дано: ΔABC, K∈AB, M∈BC, KM║AC,
BK = 4 см, АК = КМ = 6 см, МС = 9 см
Найти:
Решение:
Так как KM║AC, то по расширенной теореме Фалеса:
BM = 6 см
AB = AK + BK = 6 + 4 = 10 см
BC = BM + MC = 6 + 9 = 15 см
Рассмотрим ΔABC и ΔKBM.
∠B - общий, ∠А = ∠BKM как соответственные углы при KM║AC и секущей АВ. Следовательно, треугольники подобны по двум равным углам:
ΔABC ~ ΔKBM.
AC = 15 см
см
Ответ: 40 см.
Приложения:
Похожие вопросы
Предмет: История,
автор: kamilabicekueva
Предмет: Математика,
автор: Evgen4k12
Предмет: Право,
автор: r0m125
Предмет: Физика,
автор: Lizunchik5353