Предмет: Геометрия,
автор: Sharibjanovaalya
ПОМОГИТЕ срочно!!!! 20 баллов
Геометрия задача 877!!!!!!!!!!
Приложения:

Ответы
Автор ответа:
0
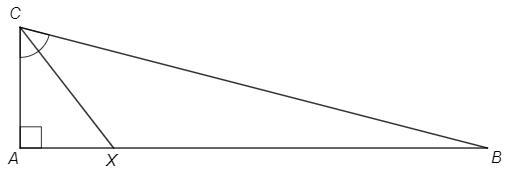
В прямоугольном треугольнике синус острого угла - отношение противолежащего катета к гипотенузе.
sinB =AC/BC =1/4
По теореме о биссектрисе
AX/BX =AC/BC =1/4
Площади треугольников с равными высотами относятся как основания.
S(ACX)/S(ACB) =AX/AB =1/5
S(ACX) =20/5 =4
Приложения:
Автор ответа:
0
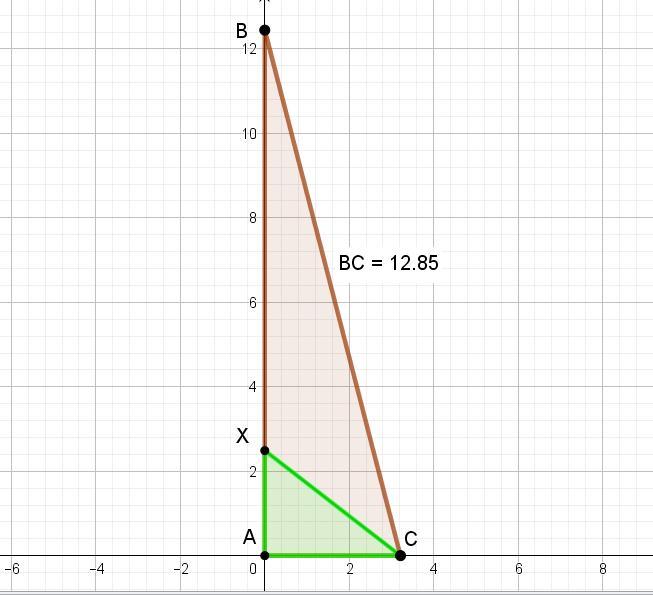
Пусть имеем прямоугольный треугольник АВС с прямым углом А.
Катет АВ = с, катет АС = в
На основе задания, где sin B = 0,25 = 1/4, получаем ВС = 4в,
По свойству биссектрисы АХ/АС = ВХ/ВС.
То есть точка Х делит АВ в отношении 1 : 4.
Треугольники АВС и АХС имеют одинаковую высоту, поэтому их площади пропорциональны отрезкам АХ и АВ.
Ответ: S(AXC) = (1/5)*20 = 4 кв.ед.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: lizayasko110220
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: mansnurllanuly
Предмет: Литература,
автор: маргофеокт