Question

Скласти рівняння кола, яке проходить через точки А(3;7) і точки В(5;-1). Центр кола на вісі ординат.

Answer 1

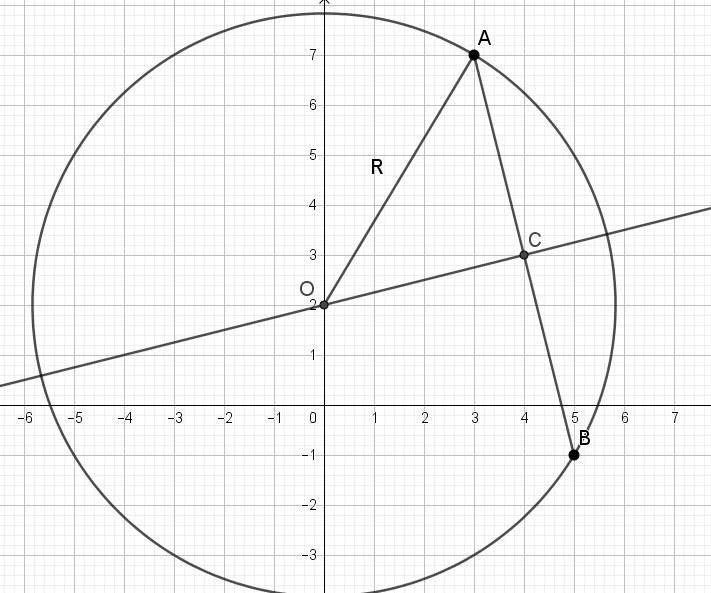
Даны точки А(3; 7) и В(5; -1). Центр окружности на оси ординат.

Центр окружности лежит на перпендикуляре к середине хорды АВ.

Уравнение АВ: (х - 3)/2 = (у - 5)/(-8). Это каноническое уравнение АВ.

Преобразуем его в уравнение с угловым коэффициентом.

у = -4х + 17.

Находим координаты середины АВ:

точка М((3+8)/2 = 4; (7-1)/2 = 3) = (4; 3).

Уравнение перпендикуляра к АВ: к = -1/(-4) = 1/4.

у = (1/4)х + в. Подставим координаты точки М: 3 = (1/4)*4 + в.

Отсюда в = 3 - 1 = 2. Получаем у = (1/4)х + 2.

Так как центр окружности на оси Оу, то х = 0.

Получили координаты центра окружности: О(0; 2).

Осталось определить радиус окружности как длину отрезка ОА = R.

R = √((3-0)² + (7-2)²) = √(9 + 25) = √34.

Ответ: уравнение окружности х² + (у - 2)² = 34.