Предмет: Геометрия,
автор: toko11037
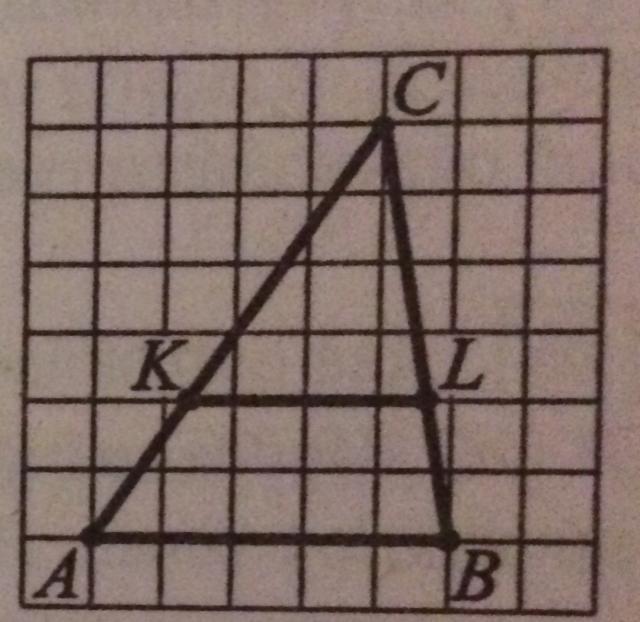
На клетчатой бумаге с размером клетки
1 см х 1 см на отрезках AC и BC отмечены точки
K и L, см. рисунок. Найдите площадь трапеции
AKLB (в см^2). Ответ округлите до сотых.
Приложения:
Ответы
Автор ответа:
1
Ответ: ≈8,33 см²
Объяснение:
На рисунке дан треугольник АВС с основанием АВ=5 см (5 клеток). Высота Н из вершины С на АВ равна 6 см. Ѕ(АВС)=6•5:2=15 см²
КL║АВ и отсекает от ∆ АВС подобный ему треугольник СКL, высота h которого 4 см. ⇒ коэффициент подобия k=h:H=4/6=2/3
Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Ѕ(CKL):S(ABC)=k²=4/9 ⇒
S(CKL):15=4/9 , откуда 9•S(CKL)=60 ⇒
S(CKL)=60/9=20/3 (см²)
Ѕ трапеции АКLB= S(ABC)-S(KCL)=15-(20/3)=25/3=8,(3)≈8,33 см²
toko11037:
Спасибо огромное!
Похожие вопросы
Предмет: Оʻzbek tili,
автор: alibekusupov20156
Предмет: Математика,
автор: evelinausenko2010
Предмет: Математика,
автор: ingachitunidze
Предмет: История,
автор: stoliarova95