Предмет: Математика,
автор: olla2004
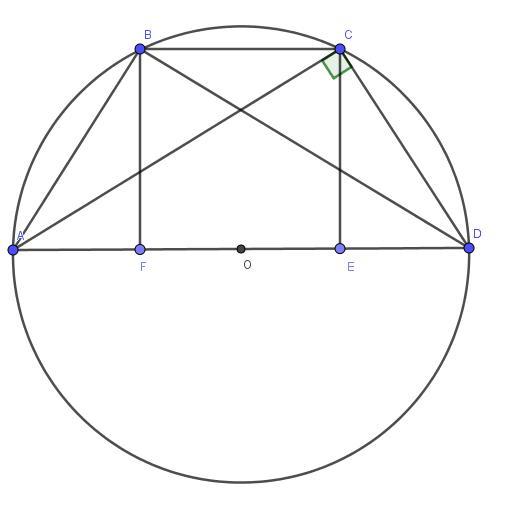
Діагональ рівнобічної трапеції перпендикулярна до бічної сторони і дорівнює 4 см. Знайдіть площу трапеції, якщо радіус кола, описаного навколо неї, дорівнює 2,5 см.
Ответы
Автор ответа:
7
Поскольку диагонали перпендикулярны к боковой стороне, то ∠ABD и ∠ACD опираются на диаметр AD, следовательно, центр окружности лежит на середине AD
AO = OD = 2.5 см, тогда AD = 2 * 2.5 = 5 см
По теореме Пифагора из прямоугольного треугольника ACD
см
Каждый катет есть среднее пропорциональное между проекцией катета и гипотенузы, т.е.
Тогда BC = AD - 2 * ED = 5 - 2 * 1.8 = 1.4 см
AE = AD - ED = 5 - 1.8 = 3.2 см
Высота, опущенная из вершины прямого угла к гипотенузе есть среднее пропорциональное между проекциями катетов
Площадь равнобокой трапеции:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Rendik13
Предмет: Математика,
автор: sofiakrasnova844
Предмет: Українська мова,
автор: Shanxz
Предмет: Математика,
автор: tanyapanova1
Предмет: Математика,
автор: анна12132