Предмет: Геометрия,
автор: pavel3563
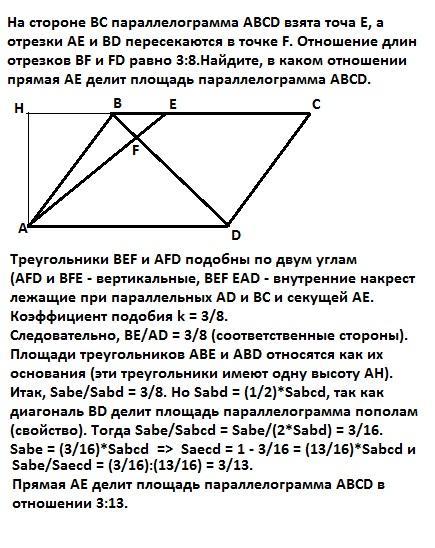
На стороне ВС параллелограмма АВCD взята точа Е, а отрезки АЕ и ВD пересекаются в точке F.Отношение длин отрезков BF и FD равно 3:8.Найдите, в каком отношении прямая АЕ делит площадь параллелограмма АВCD. (С рисунком пожалуйста)
Ответы
Автор ответа:
0
Ответ:
Прямая АЕ делит площадь параллелограмма ABCD в отношении 3:13.
Объяснение:
Треугольники BEF и AFD подобны по двум углам (∠AFD и ∠BFE - вертикальные, ∠BEF и ∠EAD - внутренние накрест лежащие при параллельных AD и BC и секущей АЕ. Коэффициент подобия
k = 3/8.
Следовательно, ВЕ/AD = 3/8 (соответственные стороны).
Площади треугольников АВЕ и ABD относятся как их основания (эти треугольники имеют одну высоту АН).
Итак, Sabe/Sabd = 3/8. Но Sabd = (1/2)*Sabcd, так как диагональ BD делит площадь параллелограмма пополам (свойство). Тогда Sabe/Sabсd = Sabe/(2*Sabd) = 3/16.
Sabe = (3/16)*Sabсd => Saeсd = 1 - 3/16 = (13/16)*Sabcd и
Sabe/Saесd = (3/16):(13/16) = 3/13.
Прямая АЕ делит площадь параллелограмма ABCD в отношении 3:13.
Приложения:
Похожие вопросы
Предмет: Химия,
автор: seludanovaleksej
Предмет: Обществознание,
автор: krutfan148
Предмет: Алгебра,
автор: hsnaoao
Предмет: Алгебра,
автор: Iskander69
Предмет: Биология,
автор: olya90494