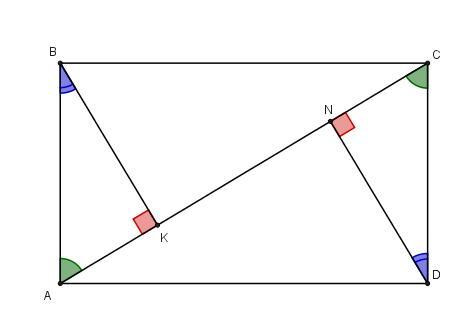
Пусть ABCD - прямоугольник, BK и DN - высоты треугольников ABC и ACD соответственно, KN = 5 см, BK = 6 см. Найдите площадь прямоугольника ABCD.
Ответы
∠BAC = ∠ACD как накрест лежащие углы при AB || CD и секущей AC.
AB = CD, следовательно, ΔABK = ΔCND по гипотенузе и острому углу
У равных треугольников соответствующие элементы (стороны, углы) равны, т.е. BK = DN; CN = AK.
Рассмотрим прямоугольный треугольник BKC: по т. Пифагора
(*)
Рассмотрим прямоугольный треугольник ABC: по т. Пифагора
Подставляем теперь в равенство (*), получаем
AB² найдем по теореме Пифагора из прямоугольного треугольника ABK, значит
Все данные у нас есть, осталось решить уравнение
Получили квадратное уравнение, которое можно решить через дискриминант
- не удовлетворяет условию
см
Следовательно, AC = 2*4 + 5 = 13 см, тогда
см²
см²
Второй способ решения:
У треугольников ABK и BKC прямые углы равны и ∠ABK = ∠BCK, следовательно, ΔABK ~ ΔBKC, из подобия треугольников следует, что BK/CK = AK/BK
Такое же уравнение как в первом способе.
Ответ: 78 см².