Question

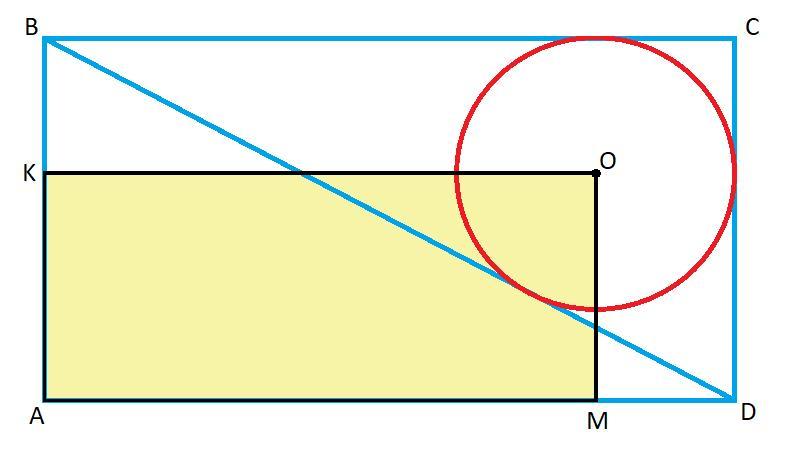
ABCD - прямоугольник (рис.), в треугольник ВСD вписана окружность с центром О. Докажите, что площадь прямоугольника AKOM равна половине площади прямоугольника ABCD.

Answer 1

Пусть CD = а, BC = b, BD = c, тогда r = (a + b - c)/2

OM = AB - r = a  -   (a + b - c)/2 = (a + c - b)/2

KO = BC - r = b  -  (a + b - c)/2 = (b + c - a)/2

S (akom) = OM•KO = ( c + (a - b) )/2  • ( c - (a - b) )/2 = (c² - (a - b)²)/4 =

= (c² - a² + 2ab - b²)/4 = (a² + b² - a² + 2ab - b²)/4 = 2ab/4 = ab/2 , ч.т.д.

Answer 2

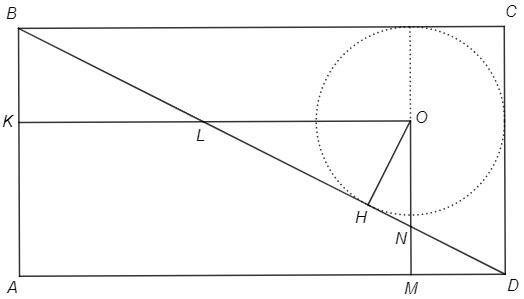
Проведем радиус OH в точку касания на диагонали.

BK=OH (расстояние между параллельными BC и KO равно радиусу)

△BLK=△OLH (по катету и острому углу)

Аналогично △NDM=△NOH

S(NLO)=S(BLK)+S(NDM)

Следовательно S(AKOM)=S(ABD)=S(ABCD)/2