Question

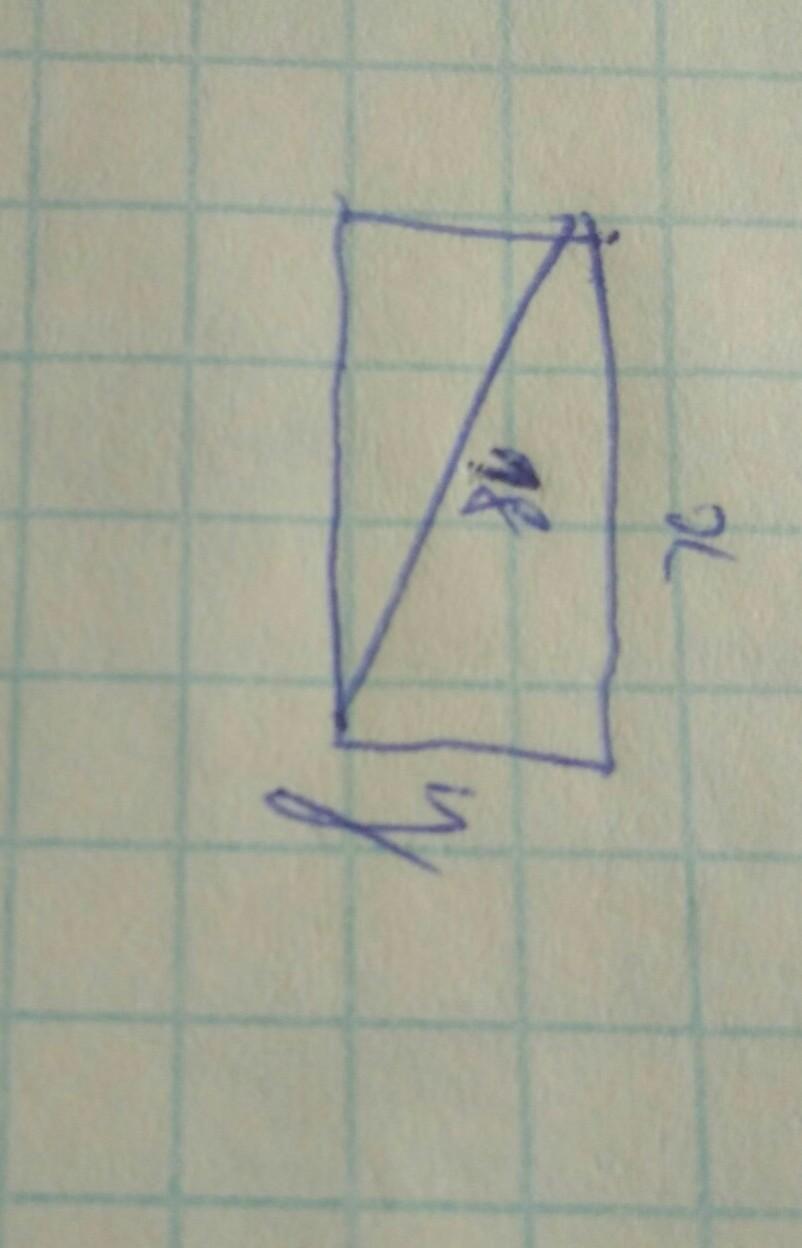
Нужно найти максимально значение площади этого прямоугольника с помощью составления функции ну и производной. Если что то там 18​

Answer 1

Ответ: 162

Объяснение: S=xy

x^2+y^2=18^2 => y=sqrt(18^2-x^2)

S(x)=x×sqrt(18^2-x^2)

S(x)'=(18^2-2x^2)/sqrt(18^2-x^2)

Находим точки экстремума:

S(x)'=0 => x=+-9sqrt(2)

Максимальное значение функция достигает когда x=9sqrt(2) (и это равно y, т.е фигура-квадрат).

S=(9sqrt(2))^2=162

Answer 2

по т пифагора

x^2+y^2=18^2

y=√(18^2-x^2)

S=xy=x√(18^2-x^2)

максимум. экстремум нахожу через S`=0

S`=√(18^2-x^2)+x*(-2x)/(2√(18^2-x^2)

√(18^2-x^2)=x^2/√(18^2-x^2)

x^2=18^2-x^2

2x^2=324

x^2=162

x=√162=9√2

y^2=18^2-x^2=324-162=162

y=√162=9√2

Тогда максимальная площадь прямоугольника

S=(9√2)^2=162