Предмет: Алгебра,
автор: dfgrtyhdg2112433
помогите решить пж 20 баллов
Приложения:
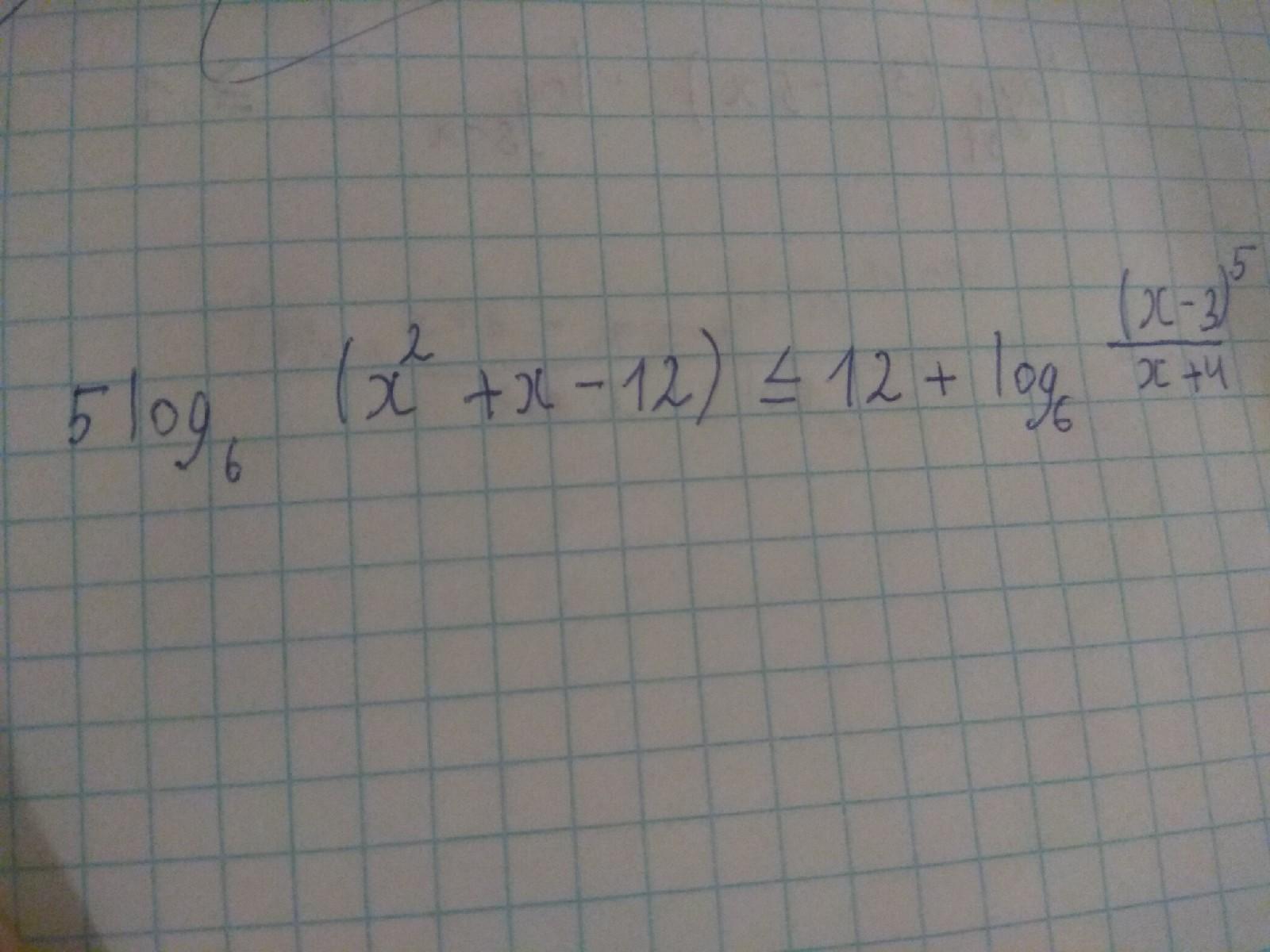
Аноним:
Такое себе задание, методом разложения на множители пойдет
Вышло [-40;-4) U (3;32]
Senpay908, решайте! Свободно!
Сейчас приготовлю )
Ответы
Автор ответа:
1
Объяснение:
как же, я увидел)
где?
6*log(x+4) = log(x+4)^6 <= log6 (6^(12))
(x+4)^6 <= 6^12
|x+4| <= 6^2
-36 <= x+4 <= 36
-40 <= x <= 32
(x+4)^6 <= 6^12
|x+4| <= 6^2
-36 <= x+4 <= 36
-40 <= x <= 32
а почему нельзя сократить на 6 ?
т.к. для x < -4 и выражение (x-3)<0 и (x+4)<0 и под логарифмом они (эти выражения) находиться не могут... lg(x^2) = 2*lg(|x|)
Автор ответа:
2
Ответ: x ∈ [-40; -4) ∪ (3;32].
Объяснение:
Приложения:

Похожие вопросы
Предмет: Биология,
автор: viperdodge3109
Предмет: Литература,
автор: PicNics333
Предмет: Алгебра,
автор: Geenii850
Предмет: Литература,
автор: tsarviktoriia
Предмет: Литература,
автор: мидашка1