Question

Составить уравнение по задаче.
Условие: На каждой из сторон прямоугольника построен квадрат. Сумма площядей квадратов равна 122 см^2. Найдите стороны прямоугольника, если известно, что его площядь равна 30 см^2.​

Answer 1

Ответ:

5см и 6см

Объяснение:

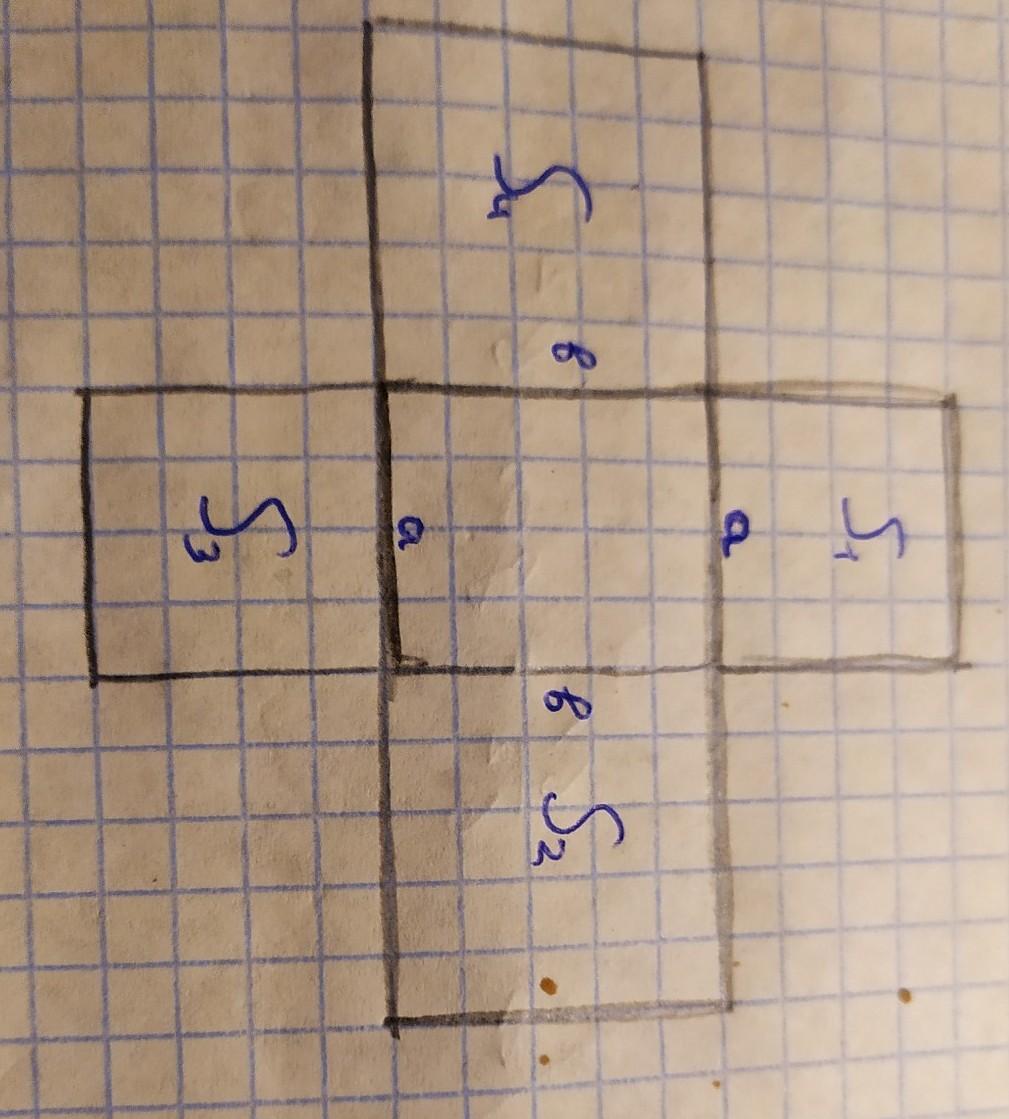
Так как нам дан прямоугольник, то это значит, что его противоположные стороны равны. Отсюда: S1=S3=a ^2, S2=S4=b^2.

Так же нам известно, что площадь прямоугольника равна 30см^2, а сумма площадей квадратов равна 122см^2.

Составим систему уравнений.

$( {a}^{2} + {b}^{2}) \times 2 = 122 \\ a \times b = 30$

Теперь разделим первое уравнение на 2, а второе возведем в квадрат.

${a}^{2} + {b}^{2} = 61 \\ {a}^{2} \times {b}^{2} = 900$

Выразим а^2 в обоих уравнениях.

${a}^{2} = 61 - {b}^{2 } \\ {a}^{2} = \frac{900}{ {b}^{2} }$

Очевидно, что теперь эти два уравнения можно записать в одну формулу.

$61 - {b}^{2} = \frac{900}{ {b}^{2} }$

Умножим обе части уравнения на b^2.

$61 {b}^{2} - {b}^{4} = 900$

Пусть b^2=k, тогда получим:

[tex]61k - {k}^{2} = 900 \\ {k}^{2} - 61k + 900 = 0 \\

Вот уравнение для задачи.