Предмет: Геометрия,
автор: s0807
На сторонах выпуклого четырехугольника как на
диаметрах построены четыре окружности. Доказать, что общая хорда окружностей, построенных на двух соседних сторонах, параллельна общей хорде двух других окружностей.
Ответы
Автор ответа:
0
на фото...................
Приложения:

s0807:
Если не сложно, а почему QD пер-но АС?
угол опирается на диаметр
спасибо
Автор ответа:
0
Общая хорда двух окружностей перпендикулярна линии центров. Линия центров соединяет середины сторон четырехугольника и является стороной параллелограмма Вариньона (параллельна диагонали четырехугольника).
Приложения:
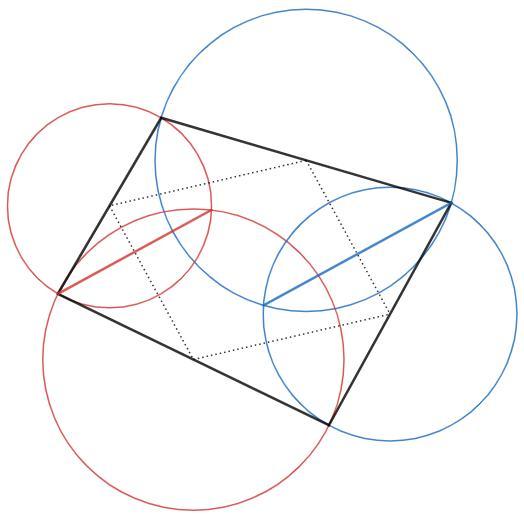
Диагональ четырехугольника делит его на два треугольника. Средние линии в этих треугольниках параллельны диагонали и равны ее половине. То есть параллельны и равны и являются противоположными сторонами параллелограмма.
Если не сложно, Линия центров соединяет середины сторон четырехугольника- это откуда видно?
А то я в геометрии не очень((
Середина диаметра - центр окружности. Если сторона четырехугольника - диаметр, то середина стороны - центр.
спасибо
Похожие вопросы
Предмет: Обществознание,
автор: iliapetlin47
Предмет: Математика,
автор: volk3456223
Предмет: Физика,
автор: vatralulia543
Предмет: Геометрия,
автор: Emma913
Предмет: Биология,
автор: RMosunov