в прямоугольном треугольнике abc катет bc равен 5 см, гипотенуза ab 13 см. на катете ac выбрана точка d, равно удаленная от точек a и b. найдите bd
Ответы
Ответ: 169/24 см
Объяснение:
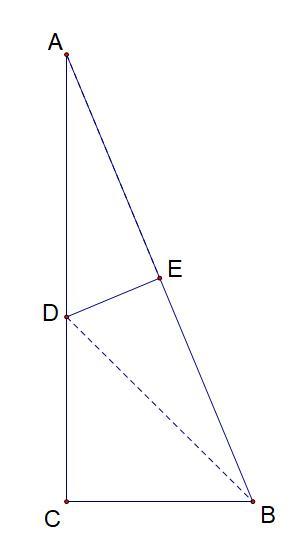
1. Точка D будет лежать на серединном перпендикуляре к стороне AB. Доказать можно так:
Построим точку D так, что AD = DB, тогда ΔADB - равнобедренный. Пусть E -- середина AB, тогда DE -- медиана, а по свойству р/б Δ является ещё высотой ΔADB.
2. AE = 1/2 AB = 1/2 * 13 = 13/2 см
По теореме Пифагора AC = 12 см
Рассмотрим ΔABC и ΔADE:
1) ∠A -- общий
2) ∠AED = ∠ACB
Следовательно, треугольники ABC и ADE подобны по двум углам.
k = AE : AC = 13/2 : 12 = 13/24 см
k = AD : AB = 13/24 см
AD = 13/24 * AB = 13/24 * 13 = 169/24 см = BD
1) для тр. АВС по т. Пифагора АС^2=АВ^2-ВС^2=13^2-5^2=144, АС=12(см).
2) АD=BD=x, DC=12-х.
Для тр. DCB по т. Пифагора
DС^2+BC^2=BD^2,
(12-x)^2+5^2=x^2,
144-24x+x^2+25=x^2,
24x=169,
x=169/24=7 1/24(см)-BD
Ответ: 7 1/24
Семь целых одна двадцать четвёртая.