Предмет: Алгебра,
автор: 15п465п465
Пожалуйста помогите решите уравнение 2 sin^x+5cos(3π/2-х)-3 все это выражение/корень из (х+5π/6)(2π-х)=0
LFP:
лучше фото уравнения... знаменатель не очень понятен...
весь знаменатель под квадратным корнем
и в знаменателе в первой скобке x не входит в числитель
в числителе в последней скобке x не входит в числитель
спс... это важно)
Ответы
Автор ответа:
0
единственная примененная тригонометрическая формула:
уравнение имеет два решения.
Приложения:
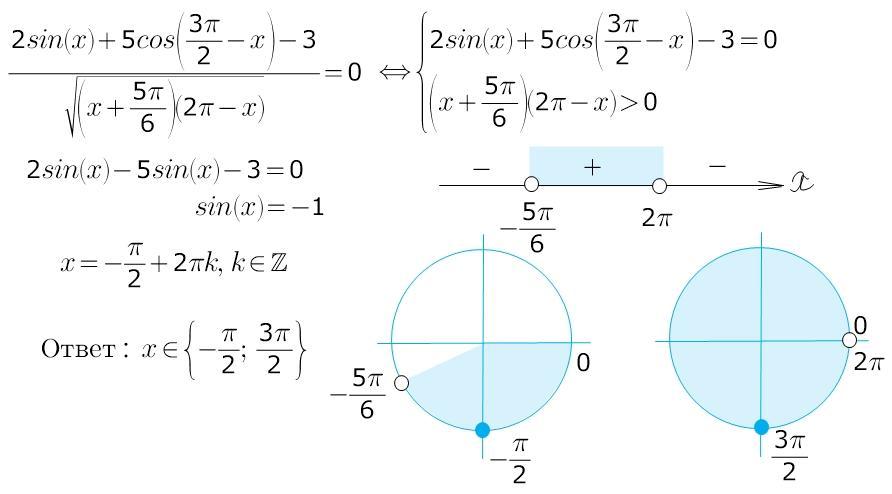
Автор ответа:
0
Если я правильно понимаю, то
Решаем неравенство методом интервалов, при x коэффициент 1, значит, в крайнем правом промежутке "+", а дальше знаки чередуются, т.к. в скобках при х нечетная степень (первая). Получаем
Это уже будет к отбору корней.
Теперь решим само уравнение:
Осталось только отобрать корни по условию
Из отрицательных корней (k=0)
Далее k=1: не подходит
При k=2
При k=-1: не подходит
Ответ:
Похожие вопросы
Предмет: Обществознание,
автор: ATMATM
Предмет: Английский язык,
автор: Jdhfjdjc
Предмет: Математика,
автор: Osmanzi2808
Предмет: История,
автор: няшнаяМилаха
Предмет: Литература,
автор: Саша11159754235