Предмет: Алгебра,
автор: ztt25
Задание на фото, срочно
Приложения:
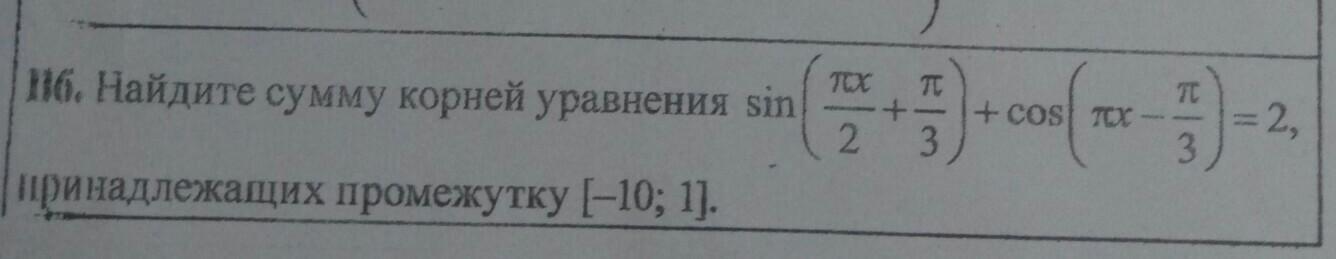
Ответы
Автор ответа:
1
Так как синус и косинус ограниченные функции и не превышаю 1, то сумма синуса и косинуса равна 2 только в том случае, если каждое слагаемое равно 1.
Система
Корни, принадлежащие отрезку [-10;1]:
x₁=(-23/3) при k=-2, n=-4
x₂=(-11/3) при k=-1; n=-2
x₃=(1/3) при k=0; n=0
x₁+x₂+x₃=(-33/3)=-11
ztt25:
почему не подбирались возможные корни, там где x=2n+1/3?
Почему не подбирались, подбирались, но система же нужно пересечение ответов. Оно есть.
ой, просите. не заметила..
простите *
Похожие вопросы
Предмет: Алгебра,
автор: svecirs
Предмет: Английский язык,
автор: Aslan1318
Предмет: Қазақ тiлi,
автор: JKtalshyn
Предмет: Химия,
автор: викавита
Предмет: Биология,
автор: даша2423