помогите решить 25 баллов
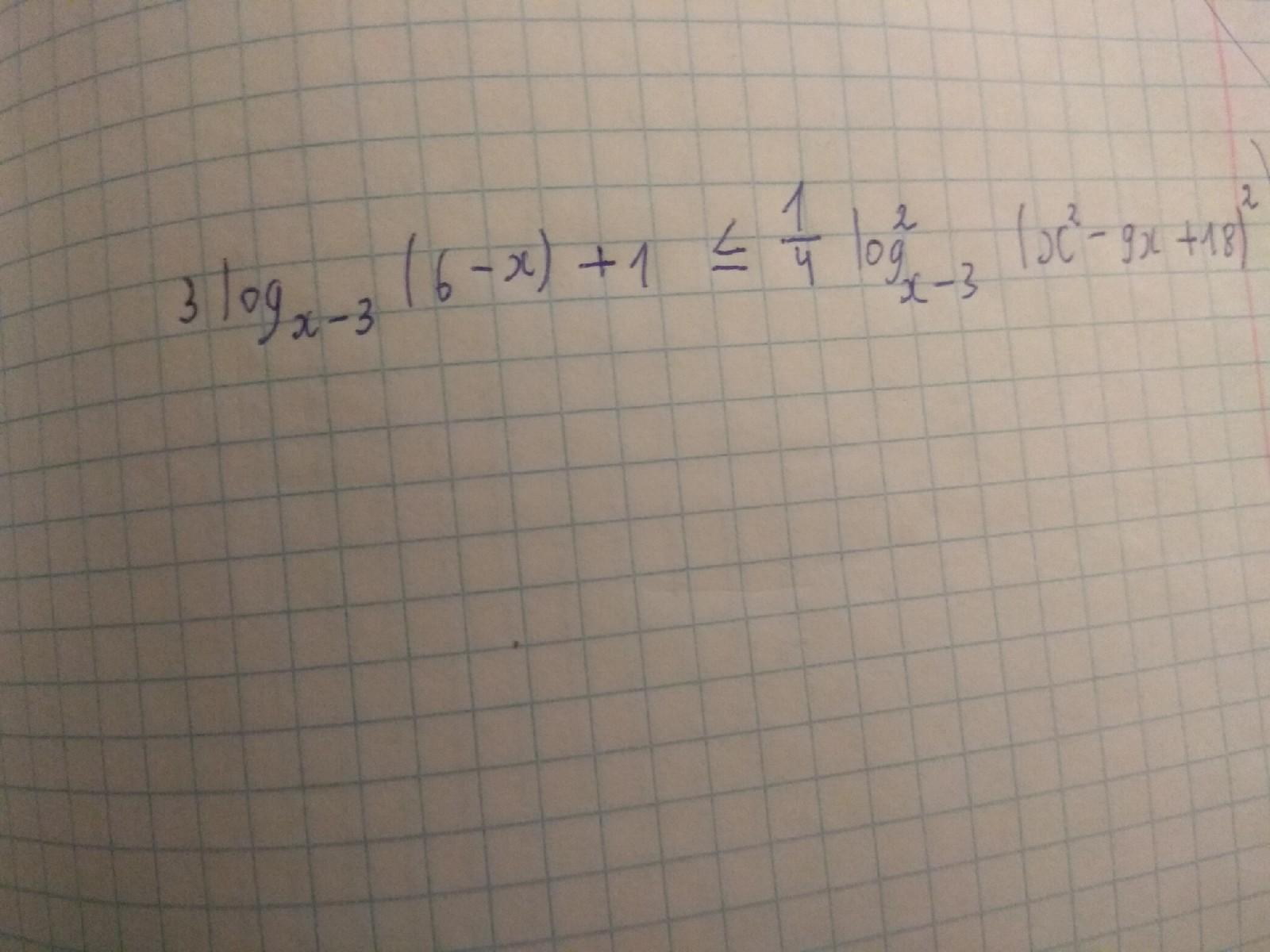
Ответы
Первым делом составим область определения:
x-3>0 ⇒ x>3
x-3≠1 ⇒ x≠4
6-x>0 ⇒ x<6
x^2-9x+18≠0 ⇒ x≠3; x≠6
Из преобразований вроде все очевидно, раскрытие модулей на области определения происходит.
Теперь решим методом интервалов последнее неравенство.
Нули f(t)=t(t-1): t=0 и t=1
t∈(-∞;0]∪[1;+∞) или если на знаках неравенств (только значок системы замени значком совокупности, он будет ОБЪЕДИНЯТЬ множества результатов неравенств системы, просто в редакторе формул этого символа как-то нет, есть только матричный/массивный)
Оба неравенства проще всего решить методом рационализации.
Итак, выражение при сравнении с 0 эквивалентно выражению
при сравнении с 0.
А это же выражение при сравнении с 0 эквивалентно выражению при сравнении с 0.
Решаем:
Оба неравенства решаются методом интервалов
в 1-ом x∈(-∞;4]∪[5;+∞)
во 2-ом x∈[4;4,5]
В совокупности это x∈(-∞;4,5]∪[5;+∞)
Но учитывая область определения исходного неравенства, получим
x∈(3;4)∪(4;9/2)∪[5;6)
Ответ: ∪
∪