Предмет: Геометрия,
автор: hmagicianh12
Вот вопрос: Две окружности радиусов R и r (R>r) касаются внешним образом.
Пусть М — точка пересечения линии центров с общей касательной
названных окружностей, а К — точка касания большей окружности с
общей касательной. Найти длину отрезка МК .
Simba2017:
непонятно где к
понятно
через подобие треугольников
Ответы
Автор ответа:
2
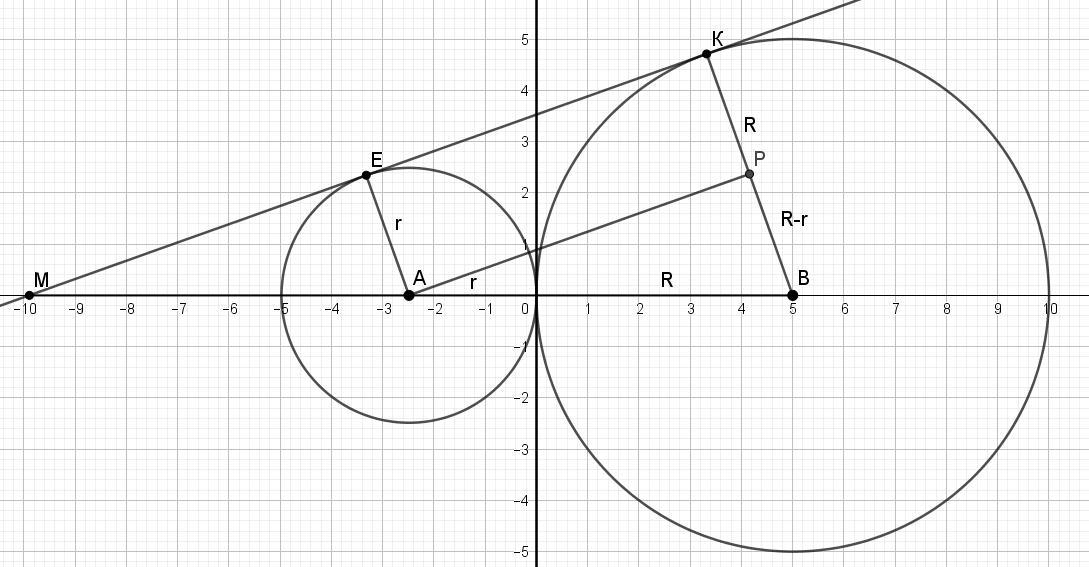
Пусть А и В - центры окружностей, точка Р - основание перпендикуляра из точки А на радиус ВК, перпендикулярный к общей касательной.
Отрезок АР = √((R + r)² - (R - r)²) = √(R² + 2Rr + r² - R² + 2Rr - r²) =
= √(4Rr) = 2√(Rr).
Тангенс угла В = АР/(R - r) = 2√(Rr)/ (R - r).
Отсюда получаем ответ: МК = R*tg B = R*2√Rr/ (R - r) = 2R√(Rr)/ (R - r).
Приложения:
Спасибо, очень помогли
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: altusha2620
Предмет: Английский язык,
автор: gachamars91
Предмет: История,
автор: Аноним