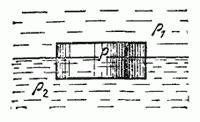
На границе раздела двух жидкостей плотности ρ1 и ρ2 плавает шайба плотности ρ (ρ1 < ρ < ρ2). Высота шайбы H. Определите глубину ее погружения во вторую жидкость.
Ответы
Ответ:
.
Объяснение:
На шайбу действуют две силы: выталкивающая сила (Архимеда) и сила тяжести. В равновесии в проекции на вертикальную ось закон Ньютона для шайбы:
FA=mg. (1) Силу Архимеда FA определим, используя соображения, приведенные при выводе закона Архимеда во введении к разделу.
Если мысленно заменить часть объема шайбы, погруженную в жидкость плотностью ρ1 самой этой жидкостью, и то же самое проделать с другой частью шайбы, то, очевидно, жидкость будет находиться в равновесии. Следовательно, мы вправе записать: FA=(Sh1ρ1+Sh2ρ2)G, (2) где S — площадь сечения шайбы, ρ2h2S — масса жидкости, заменяющая нижнюю часть шайбы, ρ1h1S - верхнюю, правая часть (2) — вес жидкости, вытесненной телом (шайбой).
Запишем также очевидные соотношения: h=h1+h2 (3) m=ρSh. (4)
Решая полученную систему уравнений (1—4), находим: h2=ρ−ρ1ρ2−ρh.
Решить задачу можно и другим способом.
Обозначим давление жидкости на верхнюю поверхность шайбы через P0, на нижнюю — P. Запишем условие равновесия мысленно выделенного столба жидкости (см. рис.) и, после несложных преобразований, получим: P=P0+(ρ1h1+ρ2h2)g.
Сила Архимеда равна: FA=PS−P0S=(ρ1h1+ρ2h2)Sg, где PS — модуль силы, действующей на шайбу вверх, P0S — вниз.
Силы со стороны жидкостей на боковую поверхность шайбы вклада в силу Архимеда не дают.
Далее решение аналогично первому способу
Ответ:
Объяснение:
1)
Пусть масса шайбы равна m.
Тогда вес шайбы в воздухе:
P = m*g= ρ*V*g = ρ*S*H*g
2)
Пусть глубина погружения шайбы во вторую жидкость равна h, тогда глубина погружения в первую жидкость (H-h)
Выталкивающие силы:
Fₐ₁ = ρ₁*g*V₁ = ρ₁*g*S*(H - h) (здесь S - площадь основания шайбы).
Аналогично:
Fₐ₂ = ρ₂*g*V₂ = ρ₂*g*S*h
Суммарная выталкивающая сила:
Fₐ = Fₐ₁+Fₐ₂ = g*S*(ρ₁*H + h*(ρ₂- ρ₁))
3)
Поскольку шайба находится в равновесии, то
Р = Fₐ
ρ*S*H*g = g*S*(ρ₁*H + h*(ρ₂- ρ₁))
ρ*H = ρ₁*H + h*(ρ₂- ρ₁)
h = H (ρ - ρ₁) / (ρ₂ - ρ₁)