Question

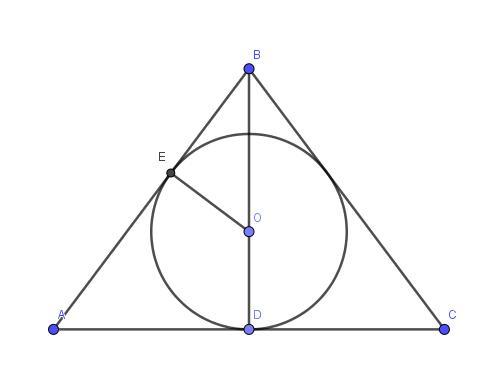
В треугольнике ABC AB=BC, точка O центр вписанной окружности, точки D и E точки касания вписанной окружности со сторонами AC и AB соответственно, угол ABC=48. Найдите угол DOE

Answer 1

Углы при основании равнобедренного треугольника:

∠BAC = ∠BCA = (180° - ∠ABC)/2 = (180° - 48°)/2 = 66°

Рассмотрим четырехугольник AEOD, известно что касательная к окружности перпендикулярная к радиусу, проведенному в точку касания, т.е. ∠AEO = ∠ADO = 90°. Сумма углов четырехугольника равна 360°

∠DOE = 360° - 66° - 90° - 90° = 114°

Ответ: 114°