Предмет: Геометрия,
автор: СкуйИМоре
Найдите AE, расписать
Приложения:

Ответы
Автор ответа:
1
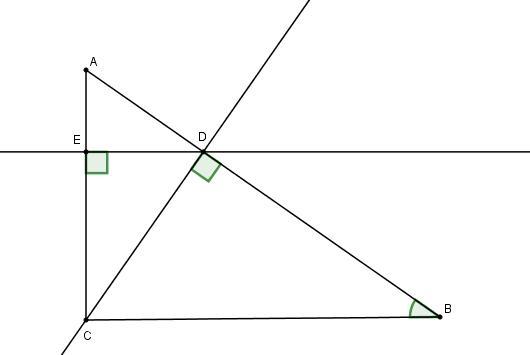
Рассмотрим прямоугольный треугольник CDB: против угла 30° катет в два раза меньше гипотенузы, т.е. BC = 2*CD = 32 см.
BD = BC * cos30° = 32 * √3/2 = 16√3 см
Высота, проведенная из вершины прямого угла есть среднее пропорциональное между проекциями катетов.
Так как ED и BC перпендикулярны к одной прямой, то ED ║ BC, следовательно, ∠ADE = ∠ABC как соответственные.
ΔAED ~ ΔCDB по двум углам. Из подобия треугольников следует, что BC/AD = CD/AE
Приложения:
Похожие вопросы
Предмет: Математика,
автор: romagolub95
Предмет: Литература,
автор: konoplenkodanil2535
Предмет: Математика,
автор: honornatalia
Предмет: География,
автор: Vilu1414