Предмет: Математика,
автор: 4epHblu
2COS^(4)4X-COS4X-3=0
РЕШИТЕ УРАВНЕНИЕ
MizoriesKun:
А второй ,cos не в квадрате разве ?
нет
Ответ x=pi/2+2pk ; x=3pi/2+2pk?
Ой, нет, x=pi/4+pik/2
Ответы
Автор ответа:
1
Ответ: x=pi/4+pik/2
Пошаговое объяснение: на фото.
Приложения:

Автор ответа:
1
2cos⁴4x - cos4x - 3 = 0
2cos⁴4x = cos4x + 3
Пусть cos4x = t, t ∈ [ - 1 ; 1 ], тогда
2t⁴ = t + 3
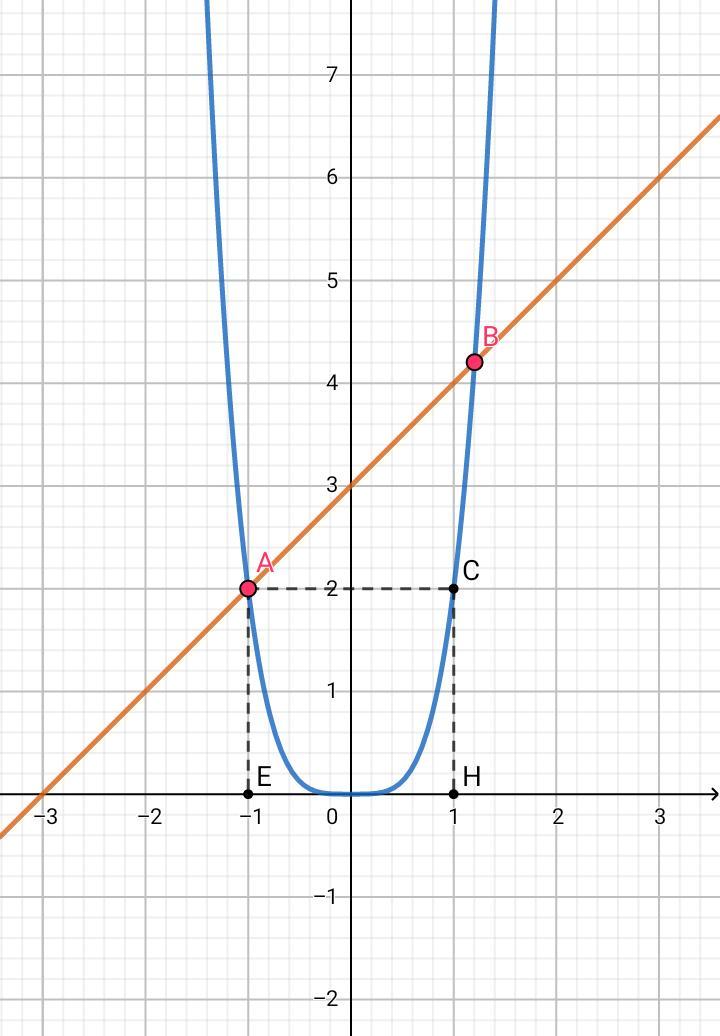
Нарисуем графики функций обеих частей уравнения:
- f(t) = 2t⁴ - синий график, чётная функция, симметричен относительно оси ординат, при t => - ∞ и + ∞ , f(t) => + ∞
- g(t) = t + 3 - оранжевый график, линейная функция, возрастающая
Графики функций пересекаются в 2 точках: А и В.
Первый корень несложно найти, t₁ = - 1 ⇒ f(t₁) = 2. Если построить точку А (-1;2) симметрично, относительно оси ординат, то попадаем в точку t₀ = С (1;2). График функции f(t) при t ≥ 0 возрастает, поэтому f(t₂) > f(t₀) ⇒ t₂ > t₀ ⇒ t₂ > 1 , но t ∈ [ - 1 ; 1 ] ⇒ ∅
t = - 1 ⇔ cos4x = - 1 ⇔ 4x = π + 2πn ⇔ x = (π/4) + (πn/2), n ∈ Z
Ответ: (π/4) + (πn/2), n ∈ Z
Приложения:
Похожие вопросы
Предмет: Математика,
автор: ssestydios
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: sansyzbay2007
Предмет: Математика,
автор: svetl6ty