Question

В прямоугольном треугольнике радиус вписанного круга равен r, острый угол альфа. Найти площадь треугольника.

Answer 1

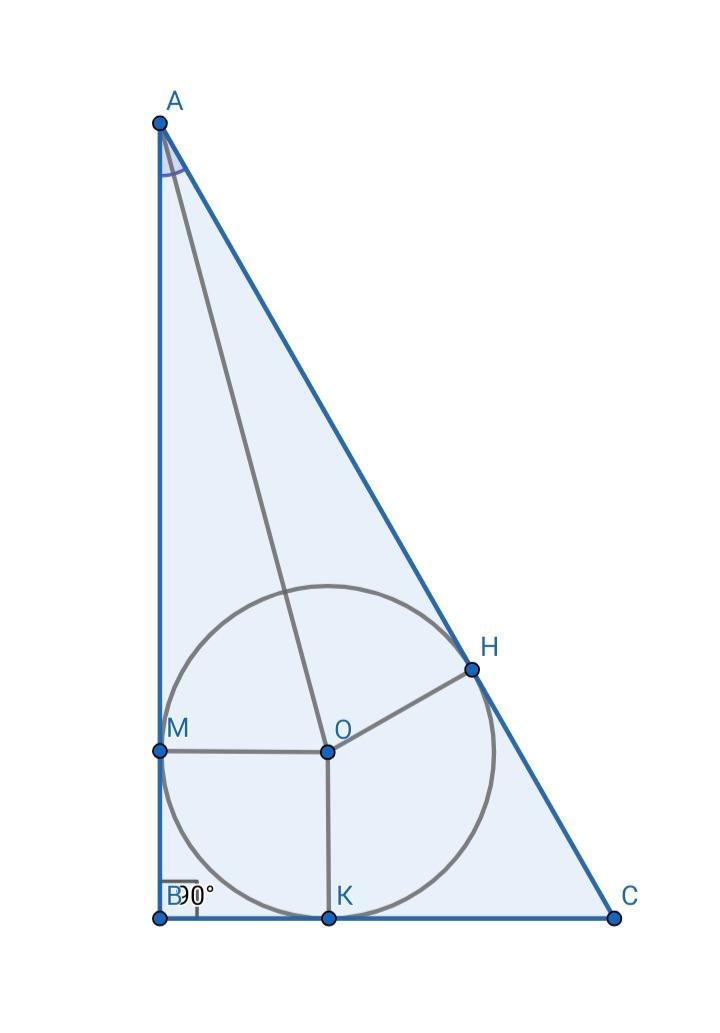
Центром вписанной окружности является точка пересечения биссектрис, поэтому АО - биссектриса ∠А, ∠МАО = ∠НАО = α/2

В ΔМАО: tg(α/2) = MO/AM ⇒ MO = r•tg(α/2), но OM⊥AB, OK⊥BC, MO = OK = r, поэтому МВКО - квадрат, МВ = ВК = r, AB = AM + BK = r•tg(α/2) + r = r•( tg(α/2) + 1)

B ΔABC: tg(α) = BC/AB ⇒ BC = AB•tg(α) = r•tg(α)•(tg(α/2) + 1)

S = (1/2)•AB•BC = (1/2)•r•( tg(α/2) + 1 )• r•tg(α)•( tg(α/2) + 1 ) =  (r²•tg(α)/2)•( (tg(α/2) + 1 )²

Ответ:  (r²•tg(α)/2)•( (tg(α/2) + 1 )²