Помогите решить 1 пожалуйста
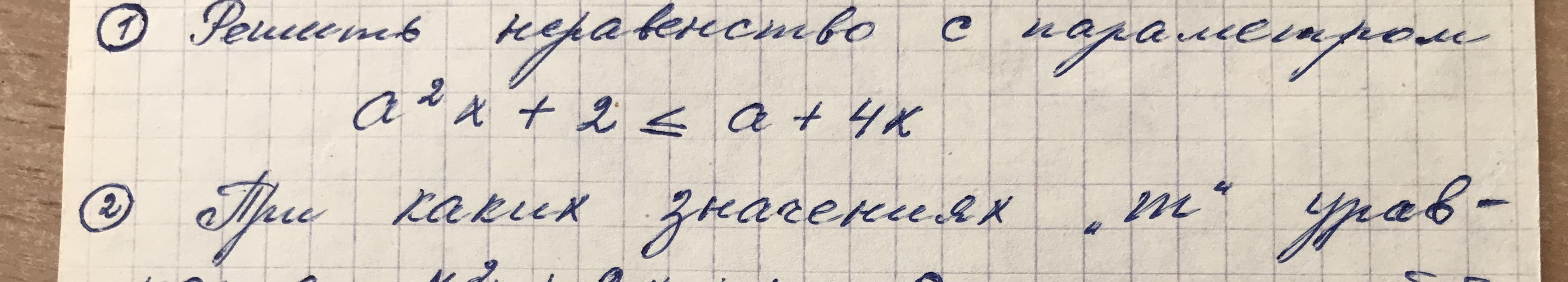
Ответы
Сначала выполним некоторые примитивные действия
Теперь уже надо рассматривать в зависимости от параметра a.
Крайний случай a = 2. Подставив его, получим верное неравенство (даже равенство), так что при a = 2 x∈R (все действительные значения)
Далее при a>2: a-2>0, поделим на эту скобку и без изменения знака
Так как a-2>0, то a+2 тем более больше 0, делим на a+2, не меняя знака
Теперь вернемся к рассмотрению случаев, когда a<2, то есть a-2<0 и деление на a-2 поменяет знак неравенства.
Крайний случай здесь a = -2. Подставим это значение в неравенство и получим 0≥1, это неверно, то есть при a = -2 x∈∅ (нет решений).
Далее рассматриваем подслучай -2<a<2, здесь a+2>0, то есть делим без изменения знака неравенства
И остался случай, когда a<-2, тогда a+2<0 и деление изменит знак неравенства
Подводя итог, получаем при a∈(-∞;-2) x≤1/(a+2); при a=-2 x∈∅;
при a∈(-2;2) x≥(a+2); при a=2 x∈R; при a∈(2;+∞) x≤1/(a+2)
Видно, что промежутки с бесконечностью можно объединить, так как решение неравенства одинаковые по написанию (можно и оставить, это как угодно, но я лично объединю)
Ответ: при ∈
∪
, при a = -2 x∈∅, при a = 2 x∈R, при
∈