Предмет: Геометрия,
автор: kapley220
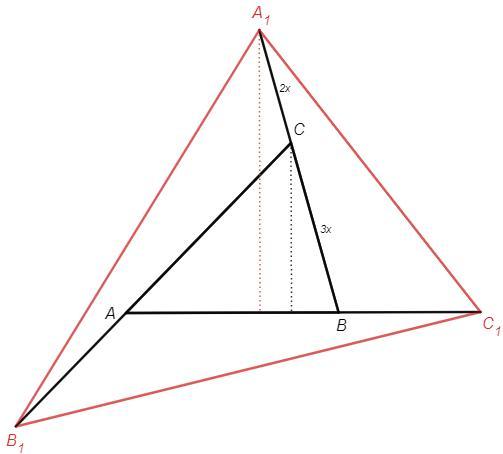
На продолжении стороны BC треугольника ABC за точку С выбрана точка A1, на продолжении стороны АС за точку А - точка В1, на продолжении стороны АВ за точку В - точка С1. Найдите отношение площади треугольника А1В1С1 к площади треугольника АВС, если |А1С|:|СВ|=|В1А|:|АС|=|С1В|:|ВА|=2:3
Ответы
Автор ответа:
3
Высоты из вершин A1 и C к прямой AB относятся как 5/3
(Высоты параллельны и отсекают от сторон угла подобные треугольники.)
Основания C1B и AB относятся как 2/3
Площади A1BC1 и ABC относятся как 5/3 *2/3 =10/9
Аналогично площади треугольников C1AB1 и B1CA1 составляют 10/9 от площади ABC.
S_A1B1C1 =S_ABC +3*10/9 S_ABC =13/3 S_ABC
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: ruslanspomer
Предмет: Алгебра,
автор: 9ineBot
Предмет: Английский язык,
автор: foxtrotport1119
Предмет: Математика,
автор: valentina2511
Предмет: Математика,
автор: Лиза1581