Question

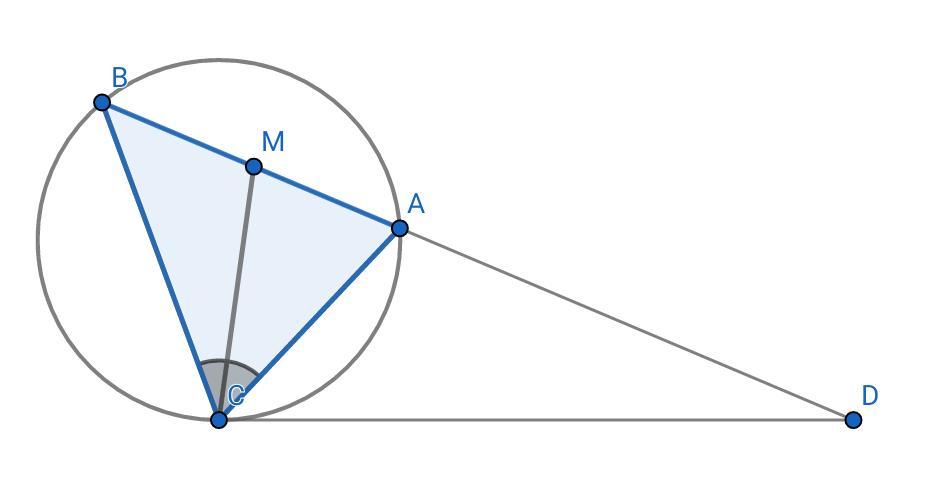
Биссектриса CМ треугольника ABC делит сторону AB на отрезки АВ = 15, МВ = 16.
касательная к окружности, описанной около треугольника АВС, проходит через точку С и пересекает прямую АВ в точке D. Найдите СD

Answer 1

ΔCAD подобен ΔBCD по двум углам:

• ∠АВС = ∠АСD - как угол между касательной CD и хордой AC
• ∠B - общий

Составим отношения сходственных сторон:

AD/CD = CD/BD = AC/BC = 15/16, по свойству биссектрисы СМ ΔАВС АС/ВС = АМ/МВ = 15/16. Пусть CD = 15x, BD = 16x, тогда AD = 16x - 31

Из подобия получаем: СD² = AD•BD ⇔ (15x)² = (16x - 31)•16x ⇔ 225x² = 256x² - 31•16x ⇔ 31x² - 31•16x = 0 ⇔ 31x•(x - 16) = 0 ⇔ x = 16

CD = 15x = 15•16 = 240

Ответ: 240