Предмет: Математика,
автор: anzhela148
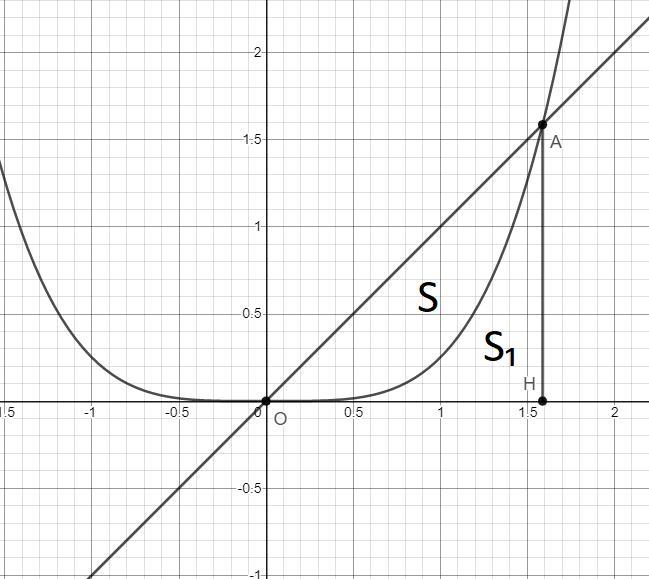
Найти площадь области, ограниченной линиями y=x, y=1/4 x^4
anzhela148:
только желательно кратко
Ответы
Автор ответа:
3
Найдем абсциссу точки A:
Ответ: ед².
Приложения:
СПАСИБО БОЛЬШОЕ!!!
ПОМОГИТЕ ЕЩЕ С ОДНИМ
Найти длину дуги кривой, заданной в полярной системе
координат уравнением p=1-cosφ, -π/3≤ φ≤-π/6
координат уравнением p=1-cosφ, -π/3≤ φ≤-π/6
Автор ответа:
0
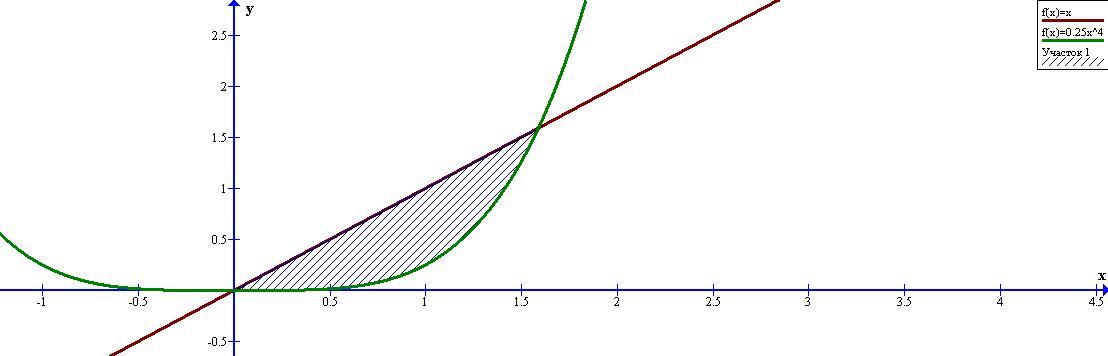
Найдем ограниченные линии, для этого приравниваем функции
Площадь ограниченной линиями:
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: anastasiakonice
Предмет: Английский язык,
автор: anakulcicka02
Предмет: Французский язык,
автор: galyusya2480
Предмет: Математика,
автор: IamLEGOman
Предмет: Алгебра,
автор: kuka5