Предмет: Алгебра,
автор: dfgrtyhdg2112433
решите пожалуйста,30 баллов
Приложения:
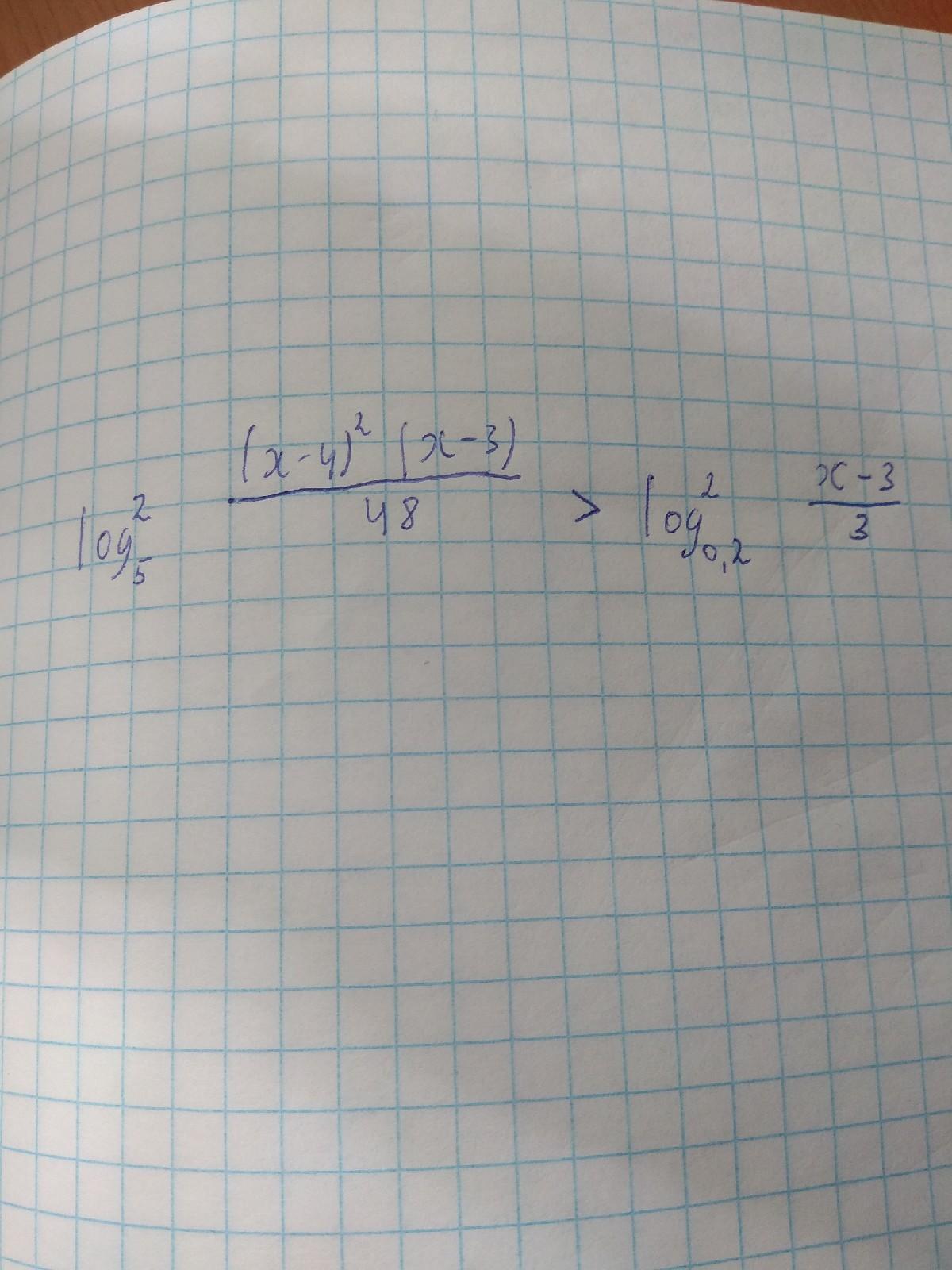
Ответы
Автор ответа:
1
ОДЗ:
Применяем метод рационализации:
Найдем пересечение и
Ответ:
ArtemCoolAc:
SmEgDm, вопрос к Вам, какие средства используете для написания ответа? Просто в стандартных, где редактор формул есть, я не видел выделения в коробочку, а также знак бесконечности, знак равносильности и др. Буду рад, если ответите
Похожие вопросы
Предмет: География,
автор: milisaerzikevic
Предмет: Английский язык,
автор: mollibarbi7
Предмет: Литература,
автор: dsffdfsfdsfdsfdsdf
Предмет: Алгебра,
автор: kseniaizmailova
Предмет: История,
автор: Sasha20032004